Learning objectives
In this code along, we will implement the engine of the Game of Life corresponding to the function hierarchy for the Game of Life (reproduced below) that we encountered when we discussed the Game of Life in the core text. We will then use the code that we wrote in the previous code along to visualize a Game of Life board in order to animate the automaton over multiple generations and see the beautiful behavior that results.
Along the way, we will also learn how to parse parameters from the command line that we can pass to the functions that we write, and apply this idea to our Game of Life program.
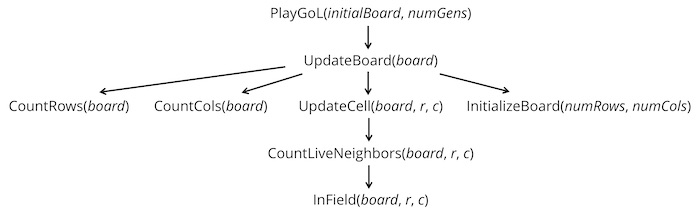
Code along summary
Setup
This code along will build upon the starter code that we built upon in the previous code along. In particular, we will be working with the game_of_life folder, which has the following structure:
boards: a directory containing.csvfiles that represent different initial Game of Life board states (more on this directory shortly).output: an initially empty directory that will contain images and MP4 videos that we draw.datatypes.py: a file that will contain type declarations (more to come shortly).functions.py: a file that will contain functions that we will write in the next code along for implementing the Game of Life.custom_io.py: a file that will contain code for reading in a Game of Life board from file.drawing.py: a file that will contain code for drawing a Game of Life board to a file.main.py: a file that will containdef main(), where we will call functions to read in Game of Life boards and then draw them.
We will be editing functions.py in this code along; at the end of the code along, we will write some code in main.py, so make sure that def main() does not have any code (it may have some code from the previous code along). Here is what our own def main() contains.
import sys
import pygame
import numpy
import imageio
from custom_io import read_board_from_file
from functions import play_game_of_life
from drawing import draw_game_board, draw_game_boards # returns list of pygame.Surface
def main():
print("Coding the Game of Life!")
if __name__ == "__main__":
main()
We will first focus on our highest level function, play_game_of_life(). This function takes as input an initial GameBoard object initial_board as well as an integer parameter num_gens indicating the number of generations in our simulation. It creates a list of num_gens+1 total GameBoard objects, sets the first one equal to initial_board, and then progressively sets boards[i] by updating the previous board boards[i-1] according to the rules of the Game of Life.
Finally, after we implement the Game of Life, we will generate an animated MP4 video visualizing the changes of a cellular automaton over multiple generations. To do so, we require importing additional packages that will allow us to generate MP4 video from collections of images.
Our highest level function: playing the Game of Life
As we will see throughout this course, although play_game_of_life() achieves something amazing, the function is quite short, passing most of the heavy lifting to a subroutine update_board() that takes a GameBoard object as input and returns the GameBoard resulting from applying the Game of Life rules to the input board over a single generation. At the start of this function, we can also practice calling our assert_rectangular() function from the previous code along.
def play_game_of_life(initial_board: GameBoard, num_gens: int) -> list[GameBoard]:
"""
Simulate Game of Life for a given number of generations.
Args:
initial_board (GameBoard): The starting game board.
num_gens (int): The number of generations to simulate.
Returns:
list[GameBoard]: A list of GameBoard objects of length num_gens + 1,
representing the progression of the game from the initial board
through each generation.
"""
if not isinstance(initial_board, list) or len(initial_board) == 0:
raise ValueError("initial_board must be a non-empty GameBoard (2D list of booleans).")
assert_rectangular(initial_board)
if len(initial_board[0]) == 0:
raise ValueError("initial_board must have at least one column.")
boards = []
boards.append(initial_board)
for i in range(num_gens):
prev_board = boards[i]
boards.append(update_board(prev_board))
return boards
Note: Recall that although we plan to visualize an animation of the Game of Life later, we are not yet drawing any of theGameBoardobjects to images, but rather storing all of the boards along the way as two-dimensional boolean lists.
Updating a single generation of the Game of Life
We next turn to implementing update_board(). As the function hierarchy indicates, update_board() relies on four subroutines, the first two of which we wrote at the end of the previous code along.
count_rows(): takes as input aGameBoardand returns the number of rows in the board.count_cols(): takes as input aGameBoardand returns the number of columns in the board.initialize_board(): takes as input integersnum_rowsandnum_colsand creates a rectangularGameBoardin which all values are set to the default value offalse.update_cell(): takes as input aGameBoardobject as well as integersrandc, and returns a boolean value corresponding to the state of the element of theGameBoardat rowrand columncin the next generation of the Game of Life.
We first call count_rows() and count_cols() to determine the number of rows and columns of the current GameBoard. Then, we initialize a GameBoard called new_board to have these same dimensions; we will eventually return new_board.
def update_board(current_board: GameBoard) -> GameBoard:
"""
update_board takes as input a GameBoard and returns the board resulting
from playing the Game of Life for one generation.
Args:
current_board (GameBoard): The current game board.
Returns:
GameBoard: A new board representing the next generation.
"""
if not isinstance(current_board, list) or len(current_board) == 0:
raise ValueError("current_board must be a non-empty GameBoard (2D list).")
assert_rectangular(current_board)
if len(current_board[0]) == 0:
raise ValueError("current_board must have at least one column.")
# first, create new board corresponding to the next generation
num_rows = count_rows(current_board)
num_cols = count_cols(current_board)
# new_board will be a new Game of Life board with every cell set to false
new_board = initialize_board(num_rows, num_cols)
# to fill in
return new_board
We then use a nested for loop to range over all the cells in the current board and update the cells of new_board. We pass current_board along with the row and column indices into a subroutine update_cell(), which returns the updated state of this cell in the next generation (as a boolean value). We then set new_board[r][c] equal to this updated state.
def update_board(current_board: GameBoard) -> GameBoard:
"""
update_board takes as input a GameBoard and returns the board resulting
from playing the Game of Life for one generation.
Args:
current_board (GameBoard): The current game board.
Returns:
GameBoard: A new board representing the next generation.
"""
if not isinstance(current_board, list) or len(current_board) == 0:
raise ValueError("current_board must be a non-empty GameBoard (2D list).")
assert_rectangular(current_board)
if len(current_board[0]) == 0:
raise ValueError("current_board must have at least one column.")
# first, create new board corresponding to the next generation
num_rows = count_rows(current_board)
num_cols = count_cols(current_board)
# new_board will be a new Game of Life board with every cell set to false
new_board = initialize_board(num_rows, num_cols)
# range through all cells of current_board and update each one
for r in range(num_rows):
for c in range(num_cols):
new_board[r][c] = update_cell(current_board, r, c)
return new_board
Updating a single cell of a Game of Life board
We now will write the two remaining subroutines initialize_board() and update_cell(), starting with the former, which is just a matter of making a GameBoard with default False values having the given number of rows and columns. Now that we are getting comfortable working with two-dimensional arrays, this task may start to feel easy.
def initialize_board(num_rows: int, num_cols: int) -> GameBoard:
"""
Initialize a GameBoard with the given number of rows and columns.
Args:
num_rows (int): Number of rows.
num_cols (int): Number of columns.
Returns:
GameBoard: A num_rows x num_cols board filled with False values.
"""
if not isinstance(num_rows, int) or num_rows <= 0:
raise ValueError("num_rows must be a positive integer.")
if not isinstance(num_cols, int) or num_cols <= 0:
raise ValueError("num_cols must be a positive integer.")
board: GameBoard = [] # declaring board
for _ in range(num_rows):
row = [False] * num_cols
board.append(row)
return board
We can then turn to implementing update_cell(), which determines the state of a cell in the next generation of the Game of Life. To do so, it first uses a subroutine to count the number of live neighbors of board[r][c], and it then applies the appropriate rule of the Game of Life based on the number of live neighbors as well as whether the cell at board[r][c] is alive. For convenience, the Game of Life rules are reproduced below.
A (Propagation): If a cell is alive and has either two or three live neighbors, then it remains alive.
B (Lack of mates): If a cell is alive and has zero or one live neighbors, then it dies out.
C (Overpopulation): If a cell is alive and has four or more live neighbors, then it dies out.
D (Rest in peace): If a cell is dead and has any number of live neighbors other than three, then it remains dead.
E (Zombie): If a cell is dead and has exactly three live neighbors, then it becomes alive.
update_cell() uses an if statement to determine if board[r][c] is alive. If so, then it considers the number of live neighbors to determine whether rule A applies, in which case we return True; otherwise, rule B or C applies, and we return False. If board[r][c] is dead, then we return True only if the number of live neighbors is 3 (rule E applies); otherwise, rule D applies, and we return False.
def update_cell(board: GameBoard, r: int, c: int) -> bool:
"""
Determine the next state of the cell at (r, c) in the Game of Life.
Args:
board (GameBoard): The current game board.
r (int): Row index.
c (int): Column index.
Returns:
bool: True if the cell is alive in the next generation, False otherwise.
"""
if not isinstance(board, list) or len(board) == 0:
raise ValueError("board must be a non-empty GameBoard (2D list).")
assert_rectangular(board)
if len(board[0]) == 0:
raise ValueError("board must have at least one column.")
num_neighbors = count_live_neighbors(board, r, c)
# apply the Game of Life rules
if board[r][c]: # cell is alive
if num_neighbors == 2 or num_neighbors == 3:
return True # survives
else:
return False # dies
else: # cell is dead
if num_neighbors == 3:
return True # becomes alive
else:
return False # stays dead
The nitty gritty: counting live neighbors of a cell
As we observed in the core text, the trickiest details are contained in the lowest levels of a function hierarchy. In particular, we should be careful when implementing count_live_neighbors(), which takes as input a GameBoard as well as integers r and c and returns the number of live neighbors in the 8-cell Moore neighborhood of board[r][c], which is reproduced in the figure below.
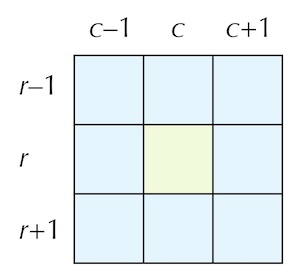
We start our implementation of count_live_neighbors() by declaring an integer variable count that will hold the number of live neighbors of board[r][c], which we will later return. To range over the Moore neighborhood of board[r][c], we will use two nested for loops, with i (our row index) ranging between r - 1 and r + 1, and j (our column index) ranging between c - 1 and c + 1.
def count_live_neighbors(board: GameBoard, r: int, c: int) -> int:
"""
Count the number of live neighbors of board[r][c], not including cells
that fall off the boundaries of the board.
Args:
board (GameBoard): The current game board.
r (int): Row index.
c (int): Column index.
Returns:
int: The number of live neighbors of board[r][c].
"""
if not isinstance(board, list) or len(board) == 0:
raise ValueError("board must be a non-empty GameBoard (2D list).")
assert_rectangular(board)
if len(board[0]) == 0:
raise ValueError("board must have at least one column.")
count = 0
# range over all cells in the neighborhood
for i in range(r - 1, r + 2): # inclusive of r+1
for j in range(c - 1, c + 2):
# to fill in
return count
We only want to include board[i][j] in the neighborhood of board[r][c] if all three of the following events occur:
board[i][j]is not the same cell asboard[r][c], which will happen when eitheri != rorj != c. We can therefore verify this with the test(i != r or j != c).board[i][j]lies within the confines ofboard, which we will check using a subroutinein_field()that returnsTrueifboard[i][j]is on the board, andFalseotherwise.board[i][j]isTrue.
If all three of these statements hold, then we will increment count by one.
Note: Python, like many programming languages, adopts short-circuit evaluation, which means that if a statement involving theandlogical connector is false, then any later statements involved as part of this connector are not evaluated. In this case, we checkin_field(board, i, j)before accessingboard[i][j]so that if this cell is not on the board, the expression will evaluate toFalseand not encounter an index out of bounds error.
def count_live_neighbors(board: GameBoard, r: int, c: int) -> int:
"""
Count the number of live neighbors of board[r][c], not including cells
that fall off the boundaries of the board.
Args:
board (GameBoard): The current game board.
r (int): Row index.
c (int): Column index.
Returns:
int: The number of live neighbors of board[r][c].
"""
if not isinstance(board, list) or len(board) == 0:
raise ValueError("board must be a non-empty GameBoard (2D list).")
assert_rectangular(board)
if len(board[0]) == 0:
raise ValueError("board must have at least one column.")
count = 0
# range over 8-cell neighborhood of board[r][c]
# in order to increment count, we need three conditions:
# 1. (i, j) != (r, c)
# 2. (i, j) inside confines of board
# 3. board[i][j] == True
for i in range(r - 1, r + 2):
for j in range(c - 1, c + 2):
if (i != r or j != c) and in_field(board, i, j) and board[i][j]:
count += 1
return count
Note: We have previously noted that nested loops can sometimes be replaced by code that uses subroutines. In this particular case, it might prove confusing to parse out the innermost if statements as subroutines.
Checking if a cell is within the confines of the board
Finally, we have reached the bottom of the function hierarchy, where in_field() is lurking. This function takes as input board as well as integers i and j. It returns True if the cell at position (i, j) is within the boundaries of board, and False otherwise.
To implement this function, we will instead check if cell (i, j) is outside the boundaries of board. This will occur if either i or j is negative, if i is greater than the number of rows in board, or if j is greater than the number of columns in board. If any of these is True, then in_field() should return False; otherwise, it should return True.
After running some parameter checks, we first check if i or j is negative by using the or connector.
def in_field(board: GameBoard, i: int, j: int) -> bool:
"""
Check if the given (i, j) indices are within the boundaries of the board.
Args:
board (GameBoard): The current game board.
i (int): Row index.
j (int): Column index.
Returns:
bool: True if (i, j) is inside the board, False otherwise.
"""
if not isinstance(board, list) or len(board) == 0:
raise ValueError("board must be a non-empty GameBoard (2D list).")
assert_rectangular(board)
if len(board[0]) == 0:
raise ValueError("board must have at least one column.")
if not isinstance(i, int) or not isinstance(j, int):
raise ValueError("i and j must be integers.")
if i < 0 or j < 0:
return False
# to fill in
Next, we check if either i is greater than the number of rows in board, or if j is greater than the number of columns in board, again using the or connector.
def in_field(board: GameBoard, i: int, j: int) -> bool:
"""
Check if the given (i, j) indices are within the boundaries of the board.
Args:
board (GameBoard): The current game board.
i (int): Row index.
j (int): Column index.
Returns:
bool: True if (i, j) is inside the board, False otherwise.
"""
if not isinstance(board, list) or len(board) == 0:
raise ValueError("board must be a non-empty GameBoard (2D list).")
assert_rectangular(board)
if len(board[0]) == 0:
raise ValueError("board must have at least one column.")
if not isinstance(i, int) or not isinstance(j, int):
raise ValueError("i and j must be integers.")
if i < 0 or j < 0:
return False
if i >= count_rows(board) or j >= count_cols(board):
return False
# to fill in
If we survive both of these checks, then we can conclude that (i, j) is within the boundaries of board, and we can safely return True as a default value.
def in_field(board: GameBoard, i: int, j: int) -> bool:
"""
Check if the given (i, j) indices are within the boundaries of the board.
Args:
board (GameBoard): The current game board.
i (int): Row index.
j (int): Column index.
Returns:
bool: True if (i, j) is inside the board, False otherwise.
"""
if not isinstance(board, list) or len(board) == 0:
raise ValueError("board must be a non-empty GameBoard (2D list).")
assert_rectangular(board)
if len(board[0]) == 0:
raise ValueError("board must have at least one column.")
if not isinstance(i, int) or not isinstance(j, int):
raise ValueError("i and j must be integers.")
if i < 0 or j < 0:
return False
if i >= count_rows(board) or j >= count_cols(board):
return False
# if we survive to here, then we are on the board
return True
Taking command line arguments with sys.argv
We are now ready to put some code into main.py to run our simulation. We will need several package imports, including custom_io (to read the initial board from a file), functions (to run the Game of Life simulation), and drawing (to render the boards as pygame.Surface objects). As a result, main.py should initially look like the following, which includes some module imports that we have not yet discussed. Note also that we only import the specific functions that we need from custom_io.py, functions.py, and drawing.py.
import sys
import pygame
import numpy
import imageio
from custom_io import read_board_from_file
from functions import play_game_of_life
from drawing import draw_game_board, draw_game_boards # returns list of pygame.Surface
def main():
print("Coding the Game of Life!")
if __name__ == "__main__":
main()
Until now, we have declared any parameters for running a simulation that we need within our code. The Game of Life offers us an opportunity to show a more advanced concept, which is allowing the user to change the parameters of the simulation themselves in the command line. Specifically, we will allow the user to change the following command line arguments at runtime.
- The name of the file containing the initial Game of Life board.
- The name of the file that will contain the final MP4 video that we draw frames to.
- The width (in pixels) of each square cell in our drawing.
- The number of generations to run the simulation.
For example, we will eventually want to run our simulation with a command like one of the following (these use the python3 command and assume that we are using macOS or Linux):
python3 main.py boards/rPentomino.csv output/rPentomino 20 1200 python3 main.py boards/dinnerTable.csv output/dinnerTable 20 60 python3 main.py boards/gosperGun.csv output/gosperGun 20 400
When code is run with command line arguments, an array of strings called sys.argv is created, with length equal to one greater than the number of parameters given. The first element, sys.argv[0], is always the name of the program (in this case, "main.py"). The remaining elements of sys.argv are strings representing the parameters passed into the program.
In the case of our first command above:
sys.argv[1]is the input CSV file (e.g.,"boards/rPentomino.csv").sys.argv[2]is the output file prefix (e.g.,"rPentomino").sys.argv[3]is the cell width, which we convert to an integer (20 in this case).sys.argv[4]is the number of generations, also converted to an integer (1200 in this case).
Since the values in sys.argv are all strings, we need to cast sys.argv[3] and sys.argv[4] to integers using int().
Let’s put this into practice in the main() function. We will first read sys.argv[1] into a variable input_csv, which will be a string representing the file location of the initial board. Next, we will read sys.argv[2] into a variable output_prefix, another string storing the prefix of the output file (e.g., the MP4 video we will generate to visualize our simulation).
def main():
print("Coding the Game of Life!")
if len(sys.argv) != 5:
raise ValueError("Usage: python main.py initial_board.csv output_prefix cell_width num_gens")
input_csv = sys.argv[1]
output_prefix = sys.argv[2]
# to fill in
Next, we will read in the width of each cell in pixels and the number of generations from sys.argv[3] and sys.argv[4]. Before storing these values in the respective variables cell_width and num_gens, we need to use int() to convert the arguments from strings to integers. Once we have done so, our work of reading parameters is finished, and we will print a statement to the console to confirm.
def main():
print("Coding the Game of Life!")
if len(sys.argv) != 5:
raise ValueError("Usage: python main.py initial_board.csv output_prefix cell_width num_gens")
input_csv = sys.argv[1]
output_prefix = sys.argv[2]
cell_width = int(sys.argv[3])
num_gens = int(sys.argv[4])
print("Parameters read in successfully!")
# to fill in
Animating the Game of Life
Now that we have read in the command line arguments, we will take the following steps:
- Read the Game of Life board from file by calling
read_board_from_file(input_csv)and store the result in aGameBoardobject calledinitial_board. - Call
play_game_of_life(initial_board, num_gens)to produce a list ofGameBoardobjectsboardscorresponding to the generations of the simulation. - Generate a list of images
surfacesby callingdraw_game_boards(boards, cell_width), which returns a list ofpygame.Surfaceobjects.
We add code to implement these steps below. To save space, we are not showing the part of def main() devoted to processing command line arguments.
def main():
# command line arguments processing...
pygame.init()
# Step 1: simulate
initial_board = read_board_from_file(input_csv)
print("Playing the automaton!")
boards = play_game_of_life(initial_board, num_gens)
# Step 2: draw surfaces
surfaces = draw_game_boards(boards, cell_width)
print("Boards drawn to images! Convert to MP4 video!")
# to fill in
Now that we have a list of image objects surfaces resulting from running the simulation, we just need to convert them into a video; to do so, we will use the imageio library. We create a writer object with imageio.get_writer(), which takes as input the target file name as a string as well as parameters corresponding to the number of frames per second (fps), the video encoding software to use (codec), and an integer between 0 and 10 (quality), where higher numbers indicate higher quality and larger file sizes. The function returns a writer object that we will use to convert surfaces into a video.
In particular, the writer object needs to convert each pygame.Surface object into an array of pixels, so that it can render the video. The array that writer desires is not a list but a special type of array called a numpy array, which occurs frequently in Python because it is optimized for arithmetic computations. Below, we convert all frames to numpy arrays using a subroutine, then close the writer, which finalizes the MP4 video file.
Finally, we add pygame.quit() to deactivate pygame modules.
def main():
# command line arguments processing...
print("Parameters read in successfully!")
pygame.init()
# Step 1: simulate
initial_board = read_board_from_file(input_csv)
print("Playing the automaton!")
boards = play_game_of_life(initial_board, num_gens)
# Step 2: draw surfaces
surfaces = draw_game_boards(boards, cell_width)
print("Boards drawn to images! Convert to MP4 video!")
# Step 3: write video
video_path = output_prefix + ".mp4"
writer = imageio.get_writer(video_path, fps=10, codec='libx264', quality=8)
for surface in surfaces:
frame = pygame_surface_to_numpy(surface)
writer.append_data(frame)
writer.close()
print("Success! MP4 video produced!")
pygame.quit()
We now will implement the pygame_surface_to_numpy() subroutine, which converts a Surface object into a numpy array so that we can save it as video. This function will be short, so we will add it to main.py.
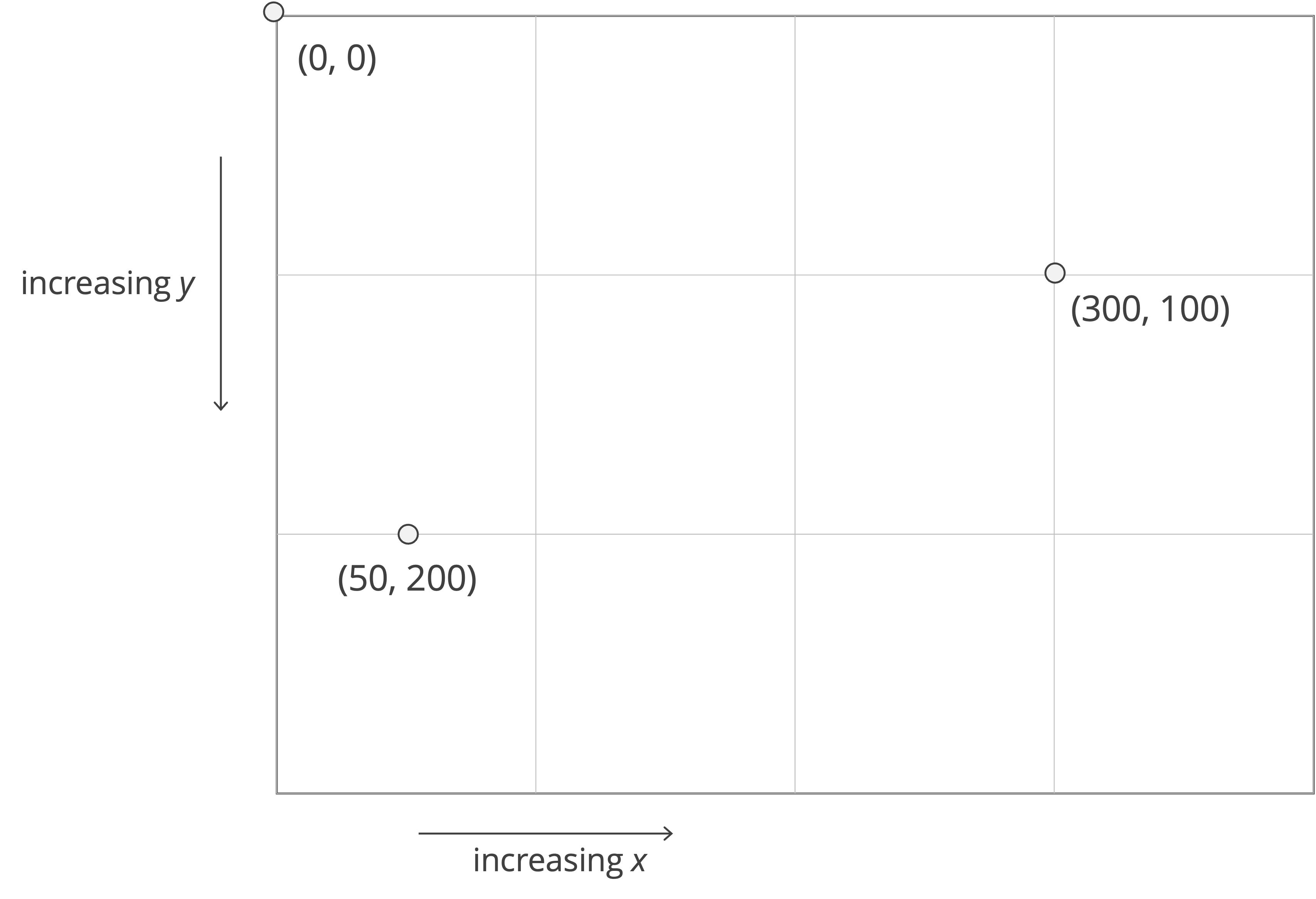
Remember from the previous code along that arrays and computer graphics follow different coordinate indexing, as shown in the figure replicated below. As a result, when we convert a pygame.Surface object to a numpy array, we need to switch the axes.
def pygame_surface_to_numpy(surface: pygame.Surface) -> numpy.ndarray:
"""
Convert a Pygame Surface to a NumPy RGB image array.
Returns:
numpy.ndarray: The frame as (height, width, 3) uint8 RGB.
"""
# get a numpy array associated with the surface and swap its axes
return pygame.surfarray.array3d(surface).swapaxes(0, 1)
Running the simulation
First, before we can run our code, we need to ensure that we have installed the following three packages. You probably installed pygame in our code along on introduction to graphics, but there is no harm in installing it again.
pygame— draws the window and grid."imageio[ffmpeg]"— lets us write MP4 videos.numpy— we need it for making the videos.
We can install all three packages with one pip command. Open a command line terminal and execute pip3 install pygame "imageio[ffmpeg]" numpy (macOS/Linux) or pip install pygame "imageio[ffmpeg]" numpy (Python). The "imageio[ffmpeg]" package looks different to the others because [ffmpeg] is an extra requirement group indicating to Pip to install any optional dependencies of imageio needed to support the ffmpeg video/audio software library.
Once we have installed these packages, we are ready to run the Game of Life.
STOP: In a new terminal window, navigate into our directory usingcd python/src/game_of_life. Then run your code by executingpython3 main.py boards/dinnerTable.csv output/dinnerTable 20 60(macOS/Linux) orpython main.py boards/dinnerTable.csv output/dinnerTable 20 60(Windows).
Running our code produces a dinnerTable.mp4 video in our output folder resembling the animated GIF shown below.

Next, we will execute the following command to animate the R pentomino. We will keep cell_width equal to 20, but we need to increase the number of generations to 1200 so that we can see the entire simulation. It may take around 20 minutes to complete (this is about 50 times slower than other languages), but the result will be worth it.
python3 main.py boards/rPentomino.csv output/rPentomino 20 1200
The result is a MP4 video like the beautiful GIF below.

Finally, we will animate the Gosper glider gun by executing the following command, which could take a minute or two to run:
python3 main.py boards/gosperGun.csv output/gosperGun 20 400
The animation of the Gosper glider gun is shown below.
Looking ahead
The Game of Life is undeniably a beaut, but our work is not done! In the next code along, we will turn our work toward implementing an arbitrary cellular automaton that can take any collection of rules. In particular, we will see one rule set called Langton’s loop that produces a self-replicating cellular automaton that will knock your socks off. Please join us, or check your work from this code along below.
Check your work from the code along
We provide autograders in the window below (or via a direct link) allowing you to check your work for the following functions:
in_field()count_live_neighbors()update_cell()update_board()play_game_of_life()



