A Reintroduction to Top-Down Programming

In this lesson, we will explore a paradigm for solving computational problems called top-down programming. In this approach, we first write a function solving the problem, assuming any subroutines that we need. We then write these subroutines, assuming any functions that they call as subroutines in turn.

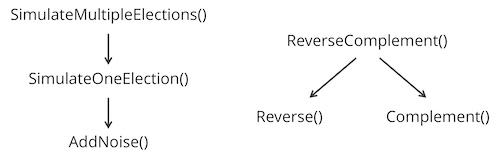
We have already used top-down programming to solve problems. In our exploration of bacterial genomes in Chapter 1, we wrote a function ReverseComplement() to take the reverse complement of a DNA string by assuming that we had two simpler functions Reverse() and Complement().

ReverseComplement(text)
    x ← Reverse(text)
    y ← Complement(x)
    return y

We also applied top-down programming when we simulated many elections by assuming that we had already written a subroutine SimulateElection() that would handle simulating a single election.

SimulateMultipleElections(polls, electoralVotes, numTrials, marginOfError)
    winCount1 ← 0
    winCount2 ← 0
    tieCount ← 0
    for numTrials total trials
        votes1,votes2 ← SimulateElection(polls, electoralVotes, marginOfError)
        if votes1 > votes2
            winCount1 ← winCount1 + 1
        else if collegeVotes2 > collegeVotes1
            winCount2 ← winCount2 + 1
        else (tie!)
            tieCount ← tieCount + 1
    probability1 ← winCount1/numTrials
    probability2 ← winCount2/numTrials
    probabilityTie ← tieCount/numTrials
    return probability1, probability2, probabilityTie

The SimulateOneElection() function in turn called an AddNoise() subroutine, which is where the gritty details of the program were hiding in the form of (pseudo)random number generation, which required its own set of subroutine calls.

As we move toward larger programs with many functions, we can visualize how these functions are organized using a function hierarchy, or a network in which functions are connected to subroutines that they call by arrows. In a function hierarchy, the “root” function (i.e., the one at the top of the diagram that has no incoming arrows) solves the computational problem at hand. Function hierarchies are shown in the figure below for the functions SimulateMultipleElections() and ReverseComplement().