Rolling a single die

Recall that to estimate the house edge of craps, we need to simulate rolling two dice. First, we will consider the simpler process of simulating a single die roll, which amounts to uniformly generating a pseudorandom number between 1 and 6.

Programming languages contain packages, or collections of pre-written code that are likely to be reused in multiple contexts. In particular, most languages have a “random” package with a built-in pseudorandom number generator. (In Go, this package, built upon the lagged Fibonacci PRNG mentioned in the previous lesson, is called rand.) A random package should, in addition to other functions, include three useful functions (although their names may vary in different languages):

  1. RandInt(): takes no inputs and returns a pseudorandom integer (within the range of integers allowable for the language and operating system).
  2. RandIntn(): takes a single integer n as input and returns a pseudorandom integer between 0 and n − 1.
  3. RandFloat(): takes no inputs and returns a pseudorandom floating-point decimal number in the interval [0, 1).
STOP: Which of these functions should we use in RollDie() to simulate rolling a die?

It may seem tempting to use RandIntn() to simulate a die roll. For example, the following version of RollDie() generates a pseudorandom integer between 0 and 5, inclusively, and then adds 1 to the resulting number.

RollDie()
    roll ← RandIntn(6)
    return roll + 1

Yet we could just as easily call RandInt() or RandFloat(). For example, if we generate a pseudorandom decimal number from [0, 1), then we can divide this interval into six equally-sized subintervals of length 1/6 and assign the die a value based on which subinterval our number falls into.

RollDie()
    roll ← RandFloat()
    if roll < 1/6
        return 1
    else if roll < 2/6
        return 2
    else if roll < 3/6
        return 3
    else if roll < 4/6
        return 4
    else if roll < 5/6
        return 5
    else
        return 6

But we could also call RandInt(), generating an arbitrary pseudorandom integer and then taking its remainder when dividing by 6 to obtain an integer between 0 and 5, inclusively. As in the preceding function, we can then add 1 to the resulting integer.

RollDie()
    roll ← RandInt()
    return Remainder(roll, 6) + 1
Exercise: Say that we have a weighted die that produces each of 1, 3, 4, and 5 with probability 1/10, and that produces each of 2 and 6 with probability 3/10. Write pseudocode for a RollWeightedDie() function that models this weighted die.

Rolling two dice

We now return to the Sum of Two Dice Problem. The table below shows the sum on two dice for each of the 36 = 6² different outcomes of rolling two six-sided dice. Assuming that the dice are fair, each of these outcomes is equally likely.

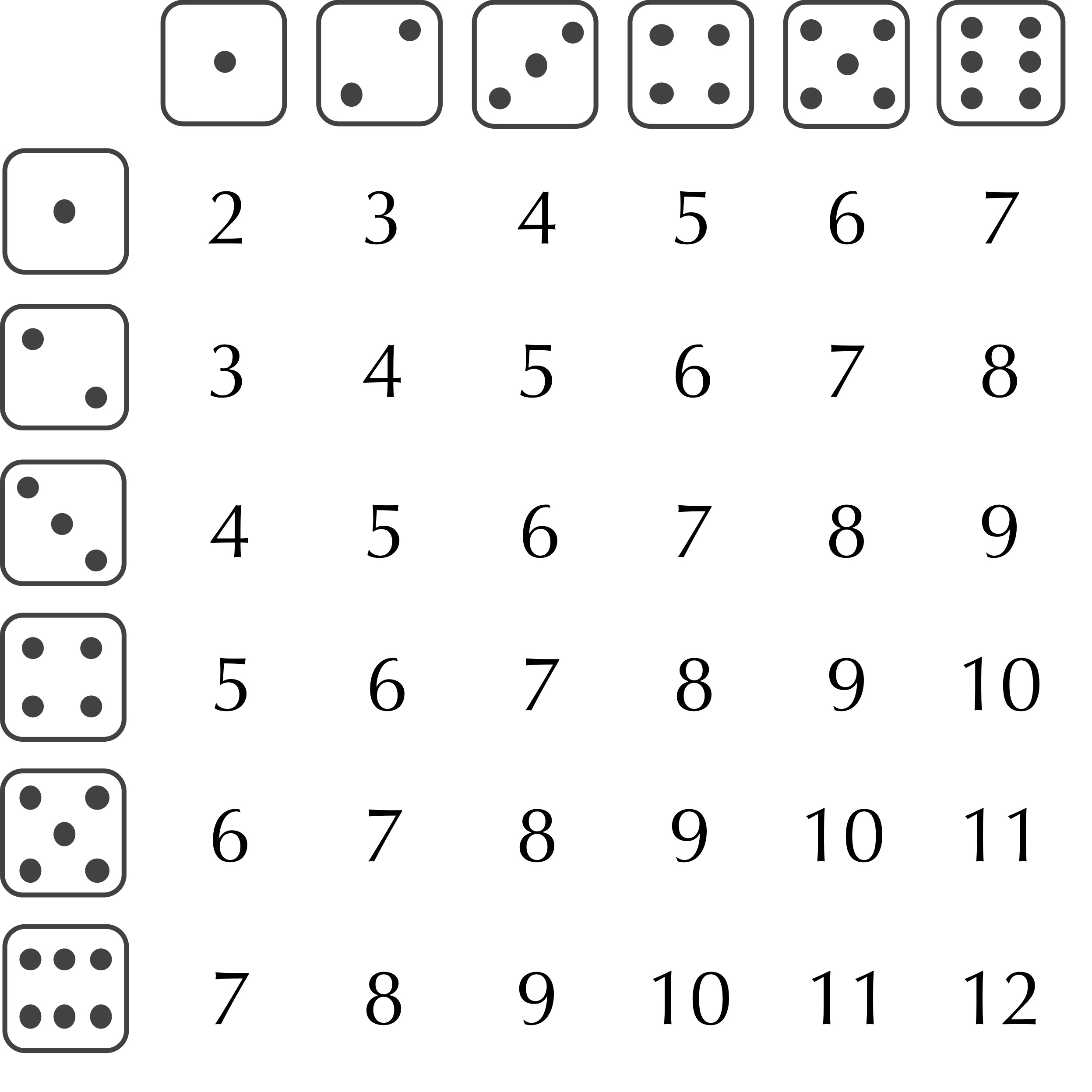
Figure: A table showing all 36 equally likely outcomes for rolling two dice and the sum of the dice for each outcome.
Exercise: Write a function SumTwoDice() that takes no input parameters and returns the simulated sum of two six-sided dice.

If we are thinking mathematically, then we would notice that the probability of rolling an x is the number of ways in which an x can be rolled, divided by the total number of outcomes (36). So, the probability of rolling a 2 is 1/36, the probability of rolling a 3 is 2/36, and so on. This reasoning leads us to apply the same principle we saw earlier before to divide the interval [0,1) into subintervals. We could divide [0,1) into 36 subintervals of equal width, but our function will be shorter if we divide [0, 1) into 11 subintervals where the width of the interval is equal to the probability that the sum of two dice will be one of the 11 integer values between 2 and 12. This idea is implemented by the following (abbreviated) pseudocode for SumTwoDice().

SumTwoDice()
    roll ← RandFloat()
    if roll < 1/36
        return 2
    else if roll < 3/36
        return 3
    else if roll < 6/36
        return 4
    ... (etc.)

We have consistently seen the power of mathematical rigor for helping us write efficient programs. But summing two dice offers an example of how we can miss a much simpler solution to a problem by being overly mathematical. In this case, modularity will make our work very easy, since rolling two dice is equivalent to rolling a single die twice.

SumTwoDice()
    return RollDie() + RollDie()
Exercise: Write a function in pseudocode called SumMultipleDice() that takes an integer numDice as input and returns the sum of the outcomes of rolling a die numDice times.

We now know enough to estimate the house edge of craps using ComputeCrapsHouseEdge() and PlayCrapsOnce(), reproduced below.

ComputeCrapsHouseEdge(numTrials)
    count ← 0
    for numTrials total trials
        outcome ← PlayCrapsOnce()
        if outcome = true
            count ← count + 1
        else
            count ← count − 1
    return count/numTrials

PlayCrapsOnce()
    firstRoll ← SumTwoDice()
    if firstRoll = 2, 3, or 12
        return false (player loses)
    else if firstRoll = 7 or 11
        return true (player wins)
    else
        while true
            newRoll ← SumTwoDice()
            if newRoll = firstRoll 
               return true
            else if newRoll = 7
                return false

Join us for this chapter’s code alongs to implement these functions. For now, we return to the chapter’s main objective of forecasting an election from polling data, where we will also see the power of modularity.

Next lesson
close

Love P4❤️? Join us and help share our journey!

Current Page

→ Page Index