Proving Euclid’s Theorem
If you are fortunate enough to be familiar with the Greek mathematician Euclid, then it is probably because of his publication of Elements, which laid the foundations of geometry around 300 BCE and still influences how the subject is taught. Yet Euclid also devised a beautiful algorithm for computing a GCD; his approach depends on the following theorem, a mathematical statement that can be proven definitively.
Euclid’s Theorem. If a and b are positive integers such that a > b, then GCD(a, b) = GCD(a − b, b).
We ask two immediate questions about Euclid’s theorem. First, how do we know that it must be true? Second, why do we really care whether it is true? That is, how can it help us devise an algorithm for computing the GCD of a and b? We will address these questions one at a time.
We start with a proof of Euclid’s theorem, or a rigorous logical demonstration that it must be true. Assume that a and b are arbitrary positive integers with a > b. Rather than show that GCD(a, b) is equal to GCD(a − b, b), we will prove a different statement, that the set of divisors shared by a and b must be the same as the set of divisors shared by a − b and b. If these two sets are the same, then certainly the largest elements in the two sets, which correspond to GCD(a,b) and GCD(a − b, b), must be the same as well.
By proving that a and b share all of the same divisors rather than just have the same greatest common divisor, it may seem that we have replaced the task at hand with a more challenging one! Yet we can prove our seemingly more difficult statement if we prove the following two statements:
- Any shared divisor of a and b must also be a divisor of a − b.
- Any shared divisor of a − b and b must also be a divisor of a.
To prove the first statement, assume that some arbitrary integer (which we will call d) is a shared divisor of a and b; we will show that d must also be a divisor of a − b. Because d is a divisor of both a and b, there must be some integers k and m such that k · d = a and m ·d = b. Subtracting the two equations gives us that k · d − m · d = a − b. Factoring d from the left side yields (k − m) · d = a − b, and so d is also a divisor of a − b, which is what we wanted to show. We assumed nothing about d other than that is was a shared divisor of a and b, so we can conclude that every such shared divisor is also a divisor of a − b.
To prove the second statement, assume that some arbitrary integer e is a shared divisor of a − b and b; we will show that e must also be a divisor of a. As before, there must be some integers p and q such that p · e = a − b and q · e = b. Certainly, a is equal to (a − b) + b, and so if we substitute p · e for a − b and q · e for b, we obtain that a = p · e + q · e = (p + q) · e. Thus, e must be a divisor of a as well.
We can now safely conclude that the set of divisors of a and b is the same as the set of divisors of a − b and b. Therefore, GCD(a, b) = GCD(a − b, b), which is what we wanted to show.
Note: Euclid’s theorem equally applies to the case that b > a, in which case GCD(a, b) = GCD(a, b − a). In other words, there is nothing special about the order of a and b.
Euclid’s algorithm for computing a GCD
Now that we have proven Euclid’s theorem, we move to our second question — how is this ancient mathematical theorem helpful for designing an algorithm to compute a GCD? Euclid noticed that we can repeatedly apply the statement of the theorem to quickly find a GCD of smaller and smaller numbers. We will see that the resulting algorithm, called Euclid’s algorithm, is much faster than the trivial approach.
We will illustrate Euclid’s algorithm with an example in which the two numbers are 378 and 273. By repeatedly applying Euclid’s theorem, we find that the GCD of these two numbers is 21, as shown below:
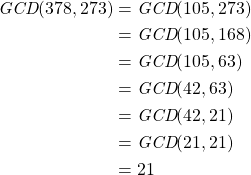
This example illustrates why Euclid’s algorithm is considered “nontrivial”. It prevents us from having to consider every possible integer up to the minimum of a and b; instead, we just make a few subtractions to determine that the GCD is 21.
Exercise: Brainstorm how we could write a function in pseudocode to compute the GCD of two numbers by repeatedly applying Euclid’s Theorem.
You might be wondering what the big deal is: Euclid’s algorithm was undoubtedly helpful to the ancient Greeks to compute GCDs by hand, but aren’t computers lightning-fast super-machines? Why does it matter what approach we use when programming a computer to find a GCD? When we implement the nontrivial algorithm and Euclid’s algorithm in a programming language, we will time the two approaches to quantify just how much faster Euclid’s algorithm is. For now, we point you to a short lecture on the importance of designing fast algorithms from computer science pioneer Grace Hopper.
Our pseudocode implementation of Euclid’s algorithm, which we call EuclidGCD()a is equal to b, and so we will use while a ≠ b as our loop. Inside the while block, we replace the larger of a or b with the positive difference between the two values. After the while loop is complete, we know that a is equal to b, and so we can return a, which must be equal to the GCD of the original parameters.
EuclidGCD(a,b)
while a ≠ b
if a > b
a ← a − b
else
b ← b − a
return a 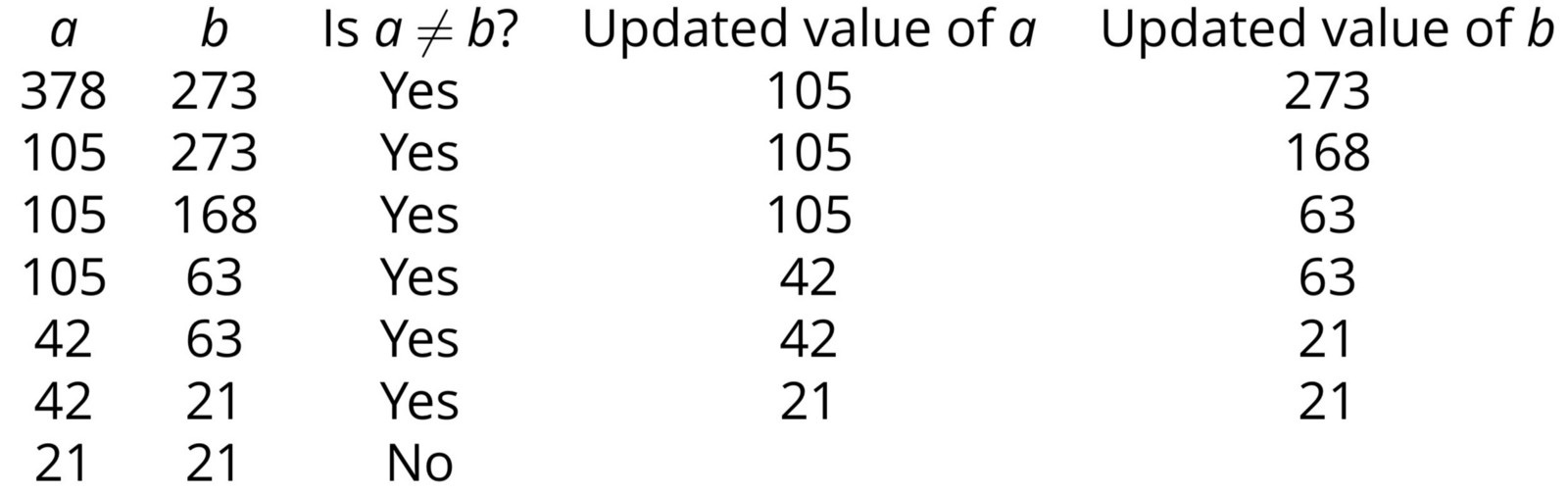
a and b are updated during EuclidGCD()STOP: If we replaced the final line inby returningEuclidGCD()binstead, how would it change the result of the algorithm?
