Chapter 2 Exercises: PRNGs and Monte Carlo Simulation

To get started, create a folder named hw2 under your go/src directory. Then create a text file named main.go inside this folder. This is the file that you should edit for the purposes of this assignment.

Timing functions on pseudorandom inputs

In Chapter 0, we saw that Euclid’s approach to computing a GCD was much faster than the trivial algorithm. (We are reproducing the pseudocode below for both algorithms for convenience.)

TrivialGCD(a, b)
    d ← 1
    m ← Min2(a,b)
    for every integer p between 1 and m
        if p is a divisor of both a and b
            d ← p
    return d
EuclidGCD(a, b)
    while a ≠ b
        if a > b
            a ← a − b
        else
            b ← b − a
    return a

We would like to quantify just how much faster Euclid’s algorithm is, but the problem is that the number of steps that it requires depends on the input values given. For example, if we compute the GCD of a = 1,000,000 and b = 1,000,000 with Euclid’s algorithm, then the while loop will never be entered, and the algorithm will immediately return 1,000,000.

Our solution is to generate two pseudorandom integers a and b in the range between some integers lowerBound and upperBound, and then to time the two algorithms on these values. We implement this idea in the window below.

Exercise: Time TrivialGCD() and EuclidGCD() for randomly chosen pairs of numbers from each of the following ranges: 1,000 to 2,000; 10,000 to 20,000; 100,000 to 200,000; and 1,000,000 to 2,000,000. What is the ratio of the runtime of TrivialGCD() to EuclidGCD() each time, and how does this ratio increase as the values of lowerBound and upperBound increase?

Warming up: weighted dies and estimating pi

Say that we would like to simulate a weighted die that has probability 0.5 in a given roll of resulting in a 3 and probability 0.1 of resulting in any of 1, 2, 4, 5, or 6.

Code Challenge: Write and implement a function WeightedDie() that models this die by taking no inputs and returning a pseudorandom integer between 1 and 6, inclusively, according to these probabilities.

You may be aware that the area of a circle is equal to the mathematical constant 𝝅 times the circle’s radius squared, but how could 𝝅 be determined? One way to do so would be to create a physical circle and measure its area using small rectangular blocks, but we will describe a way that 𝝅 can be estimated using Monte Carlo simulation.

Imagine throwing a dart at a circular dart board that is inscribed within a square (see figure below). If you were as poor of a dart player as your author, then the likelihood of the dart landing anywhere within the square (including off the board) is uniform. Under this assumption, the likelihood of the dart hitting the dartboard is equal to the ratio of the area of the circle to the area of the square.

A circular dartboard inscribed in a square. The ratio of the area of the circle to the area of the square is 𝝅/4.

Let us make the radius of the dart board be equal to 1, so that the square has side length equal to 2. As a result, the area of the circle is equal to 𝝅, and the area of the square is equal to 4, making the probability of our dart hitting the dartboard equal to 𝝅/4. We can write this as an equation:

Probability(dart hits dartboard) = 𝝅/4.

Multiplying both sides of the above equation by 4 yields an innocuous enough result:

4 · Probability(dart hits dartboard) = 𝝅.

However, if we are able to estimate the probability that the dart hits the dartboard, then we can simply multiply that estimate by 4, and it will give us an estimate for 𝝅. In this way, even if we didn’t know 𝝅, we could estimate it.

To estimate Probability(dart hits dartboard), we will apply Monte Carlo simulation. We will assume that the dartboard is centered at (0, 0), so that we can simulate throwing the dart at the square by independently generating two decimal numbers a and b that are both between -1 and 1 to obtain the point (a, b) in the square struck by the dart. The question is: how do we know whether the dart hits the circle?

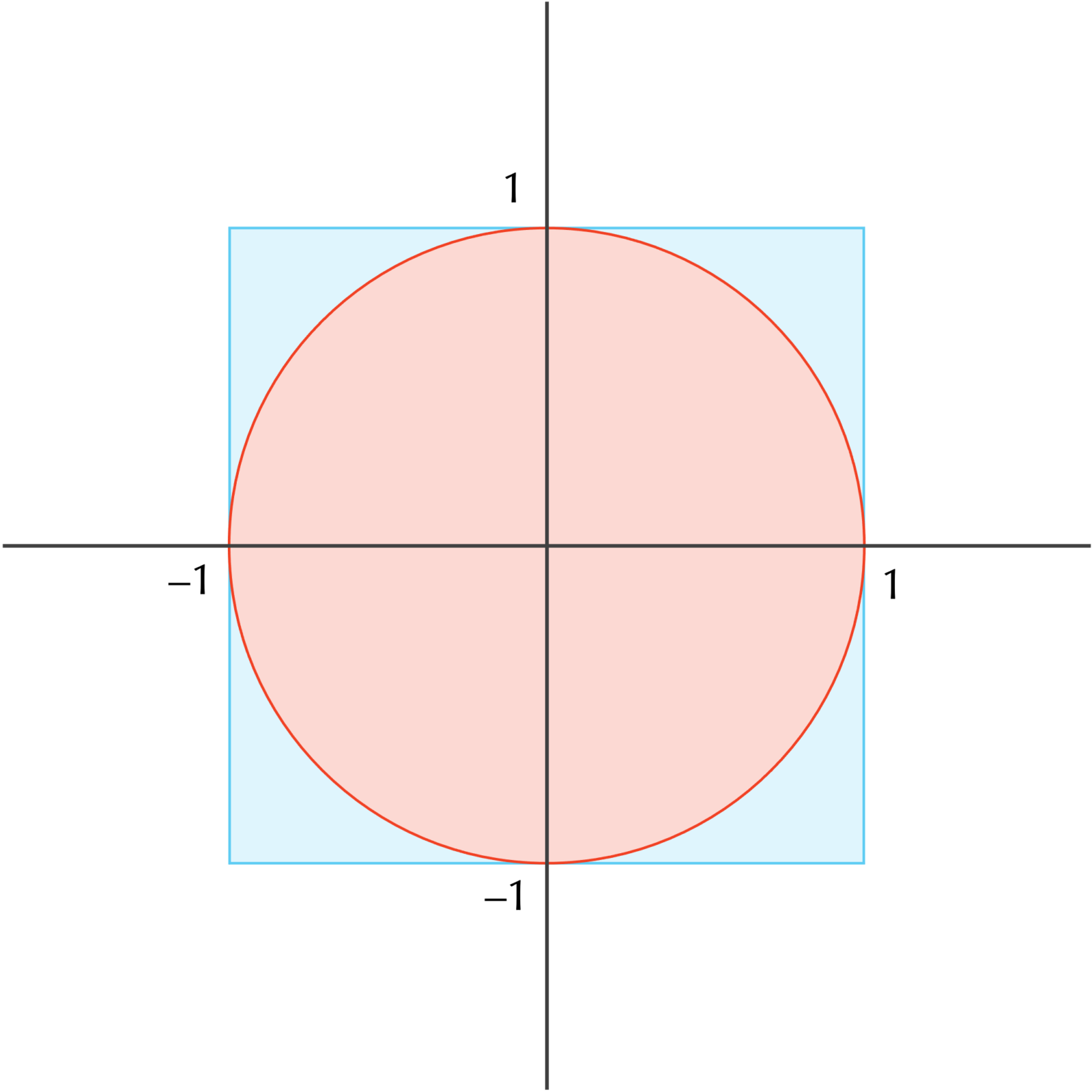
Centering our square of side length 2 at the origin means that sampling a point (a, b) uniformly from the square corresponds to independently choosing a and b as random decimal numbers between -1 and 1.

Fortunately, this question can be answered easily, since the equation for the boundary of the circle of radius 1 centered at the origin is x² + y² = 1, and a little long-forgotten high school mathematics tells us that (a, b) lies inside this boundary, and therefore on the dart board, precisely when a² + b² ≤ 1.

We can therefore iterate this process over a number of simulations, repeatedly generating a and b while counting the number of times that (a, b) falls within the circle. At the end, we can divide this count by the number of simulations to obtain an estimate for Probability(dart hits dartboard) , and as we observed above, multiplying this estimate by 4 yields our desired estimate for 𝝅.

Code Challenge: Write and implement a function EstimatePi() that takes an integer numPoints as input and returns a decimal estimating 𝝅 according to the above process of selecting numPoints points uniformly from within a square of side length 2 centered at the origin.

The following lesson allows you to check your solutions to these challenges. It can also be found using a direct link.

Estimating the probability that two integers are relatively prime

Two positive integers are called relatively prime (also called coprime) if they do not share any divisors other than 1. To determine whether two integers a and b are relatively prime, we could consult every possible divisor d between 2 and the minimum of a and b. If any such d is a shared divisor of a and b, we conclude that a and b are not relatively prime; on the other hand, if no such d is a shared divisor of a and b, then we conclude that a and b are relatively prime.

However, this sort of brute force approach of trying every possible divisor suffers from the same flaw as TrivialGCD(). Instead, we note that a and b are relatively prime precisely when their GCD is equal to 1. Accordingly, we can use our existing fast EuclidGCD() algorithm as a subroutine in order to quickly determine whether a and b are relatively prime.

Code Challenge: Write and implement a function RelativelyPrime() that takes as input two integers a and b and returns true if a and b are relatively prime and false otherwise.

A natural question is to determine the probability that two randomly selected integers are relatively prime. If we did not see a way of calculating this probability mathematically, then we could attempt to estimate the probability by generating every pair of integers in some range and counting the number of relatively prime pairs. For example, we could generate all pairs of numbers between 1 trillion and 2 trillion. However, there are about 5 · 10²³ pairs of integers in this range, and so such a brute force approach would prove prohibitively slow.

Instead, Monte Carlo simulation will provide an estimate for this probability by generating many pairs of integers in the range, testing whether each pair of integers are relatively prime, and returning the ratio of the number of relatively prime pairs to the total number of pairs considered.

Code Challenge: Write and implement a function RelativelyPrimeProbability() that takes as input three integers lowerBound, upperBound, and numPairs, and returns an estimate of the probability that two randomly chosen numbers between x and y are relatively prime by selecting numPairs pairs of numbers between lowerBound and upperBound, inclusively.

We would like to estimate the probability of any two integers being relatively prime. To do so, we would call RelativelyPrimeProbability() on a large range of integers (e.g., setting x equal to 1 and y equal to 1 trillion) and then choose many pairs of integers when testing whether given pairs are prime (e.g., setting numPairs equal to 100 million).

Exercise: Call RelativelyPrimeProbability() on your computer on a very wide range of values with lowerBound equal to 1, upperBound equal to 1 trillion, and numPairs equal to 1 billion (even with an efficient RelativelyPrime() function, your code may take a few minutes to run). What is your estimated probability that two integers are relatively prime?

Although we have estimated this probability using Monte Carlo simulation, it can be determined exactly mathematically. The correct answer is strange and beautiful, and understanding why it is the way it is relies on some very advanced mathematics. We suggest that you look it up after trying the preceding exercise.

The following lesson allows you to check your solutions to these challenges. It can also be found using a direct link.

The birthday problem

When we generate pseudorandom numbers, it is natural to think that a PRNG that produces repeated numbers is bad. After all, the brain’s method for generating “random” numbers tends to avoid repeats. But as we will see in this section, repetition is a natural component of randomness.

We can represent a sequence of random integers generated by a PRNG using an array. The following exercise will help us detect whether a sequence of integers has a repeated element.

Code Challenge: Write and implement a function HasRepeat() that takes as input an array of integers a and returns true if the array contains a repeated value and false otherwise.

Imagine a room full of people. What are the chances that there are two people in the room who share a birthday on the same day of the year? We will estimate this likelihood, which depends on the number of people in the room, using Monte Carlo simulation.

Code Challenge: Write and implement a function SharedBirthdayProbability() that takes as input two integers, numPeople and numTrials. It runs numTrials simulations and returns an estimate of the probability that in a room of numPeople people with randomly chosen birthdays, at least one pair of people have the same birthday. For simplicity, you should assume that a year always has 365 days. (Hint: the month is irrelevant when running these simulations.)

Exercise: What is the smallest value of numPeople for which there is a greater than 50% chance of two people sharing the same birthday? Are you surprised?

The following lesson allows you to check your solutions to these challenges. It can also be found using a direct link.

In a state of sin with the Middle-Square PRNG

We would like to know how we can we test the quality of a PRNG; we will apply this approach to the Middle-Square PRNG discussed in the main text, since we know that this approach is flawed.

We first would like to implement the Middle-Square PRNG, which means that we will need to write a function SquareMiddle() that takes integers x and numDigits and returns the result of squaring x and taking its middle numDigits digits. This is a simple task by hand, but how can we teach it to a computer?

First, we focus on a subroutine that we will need.

Code Challenge: Write and implement a function CountNumDigits() that takes as input an integer x and returns the number of digits in x. Your function should work for both positive and negative numbers.

Hint: first write your function for positive values of x, and then make a slight adjustment to it to accommodate negative values of x.

We can divide the process of taking the middle numDigits digits of an integer into two steps: “crossing off” the first numDigits/2 digits, then crossing off the last numDigits/2 digits. For example, we would convert the number x = 12345678 into 345678 by removing its first two digits, and then 3456 by removing its final two digits. Note that the first process corresponds to taking the remainder when we divide x by 10⁶ = 10^8-2, and the second process corresponds to taking the integer division of the resulting number by 10². In general, we can now see that we are taking the remainder of x by 10^2·numDigits^–^numDigits/2, and then dividing the resulting number by 10^numDigits/2. We only need to generalize this idea for an arbitrary value of numDigits to write SquareMiddle().

Code Challenge: Write and implement SquareMiddle(). When squaring the input number, you should add zeroes as needed to the resulting number so that it has 2 · numDigits total digits. Your function should return -1 if numDigits is odd, if x is negative, if numDigits is not positive, or if the number of digits in x is greater than numDigits. You may also find it helpful to write a subroutine Pow10() that takes as input an integer n and returns 10ⁿ.

We can now use SquareMiddle() as a subroutine in the following function, which generates the sequence of random numbers for the middle-square sequence corresponding to a given seed and number of digits.

GenerateMiddleSquareSequence(seed, numDigits)
    seq ← array of length 1
    seq[0] ← seed
    while HasRepeat(seq) is false
        seed ← SquareMiddle(seed, numDigits)
        seq ← append(seq, seed)
    return seq

Code Challenge: Implement GenerateMiddleSquareSequence().

Now that we have implemented the Middle-Square approach, we ask whether it is a good number generator. In other words, are the short sequences that we have seen this PRNG produce a general flaw? We can answer this question by determining how many seeds cause short “cycles” of numbers.

One way to determine the quality of a seed is to count the number of the sequence produced by the PRNG for this seed. However, say that our PRNG generates the sequence of numbers 140, 278, 14, 28, 19, 28, 19, 28, 19, … We could report this sequence as having length 6, the number of elements in this sequence up to the first repeat: 140, 278, 14, 28, 19, 28. However, this would be misleading, since once it generates 28, the sequence repeats the integers 28 and 19 indefinitely.

Given a seed, its period is the length of the cycle of numbers generated by a PRNG with respect to a given seed, once that cycle is produced. For this reason, in the above example, the seed 140 would have a period equal to 2, since it eventually produces a cycle containing just two elements.

We have already written a function HasRepeat() to determine whether a sequence of integers has a repeated value. If so, then we would like to compute the period of the cycle generated by these numbers.

Code Challenge: Write a function ComputePeriodLength() that takes as input an array a of integers. The function should return 0 if there are no values in a that repeat; if a has a repeated value, then the function should return the period of the sequence.

Exercise: Call GenerateMiddleSquareSequence() on every four-digit seed between 1 and 9999. How many seeds produce a sequence of period 10 or smaller? Is the Middle-Square approach a good PRNG?

The following lesson allows you to check your solutions to these challenges. It can also be found using a direct link.

Linear congruential generators

Another PRNG, called a linear congruential generator, produces the next integer y from the current integer x according to the equation

y = Remainder(a·x+c,m).

That is, we take the remainder when dividing a · x + c by m. In the linear congruential generator, a, c, and m are all constants. Different values of these constants will produce better or worse results, but a common choice is to set m equal to either a (large) prime number or a (large) power of 2.

Below, we provide pseudocode for a function GenerateLinearCongruenceSequence() that takes an initial seed as input as well as the constants a, c, and m. This function returns the sequence of integers produced by the linear congruential generator. It stops as soon as we encounter a number that we have encountered before, which means that we will need to use our function HasRepeat() as a subroutine.

GenerateLinearCongruenceSequence(seed, a, c, m)
    seq ← array of length 1
    seq[0] ← seed
    while HasRepeat(seq) is false
        seed ← Remainder(a · seed + c, m)
        seq ← append(seq, seed)
    return seq

Code Challenge: Implement GenerateLinearCongruenceSequence().

Exercise: Let a = 5, c = 1, and m = 2¹³ = 8192. What is the period when the seed is equal to 1? What can we conclude about the period of every seed between 1 and m − 1?

The following lesson allows you to check your solutions to these challenges. It can also be found using a direct link.

Up next

In this chapter, we have started encountering longer programs, with functions that call each other. As we transition to write longer programs to solve more complex tasks, we must plan carefully and organize our work.

In the next chapter, we will introduce a paradigm for planning larger coding projects called top-down programming. We will then apply this paradigm to see how to produce a simple simulation of a system that can replicate itself. Although we will cover this task in a single chapter, it took researchers 30 years to build such a system.

Continue to Chapter 3