Generating “Random” Numbers and Rolling Dice (Go)

Learning objectives

In the core text, we gained an appreciation for the pitfalls of generating pseudorandom numbers. In this code along, we will see how Go implements built-in functions for pseudorandom number generation and then apply these functions to the context of simulating dice.

Recall that we introduced the following function for rolling a single die.

RollDie()
    roll ← RandIntn(6)
    return roll + 1

The function RollDie() relies on a function RandIntn() that generates a pseudorandom number between 0 and n – 1, which we can assume is built into programming languages so that we do not need to focus on the sinful details of pseudorandom number generation.

Setup

Create a new folder called dice in your go/src directory, and then create a new file within the go/src/dice folder called main.go, which we will edit in this lesson.

Your main.go file should have the following code.

package main

import (
    "fmt"
)

func main() {
    fmt.Println("Rolling dice.")
}

Code along video

Beneath the video, we provide a detailed summary of the topics and code covered in the code along.

At the bottom of this page, you will have the opportunity to validate your work via auto-graded assessments that evaluate the functions covered in the code along.

Although we strongly suggest completing the code along on your own, you can find completed code from the code along in our course code repository.

Code along summary

Built-in pseudorandom number generation functions

Go includes functions for pseudorandom number generation via the "math/rand" package. This notation indicates that "rand" is a subdirectory of Go’s mathematics library, which should not surprise us given what we have learned about the mathematical sophistication needed to implement a PRNG.

In the main text, we introduced three functions on the level of pseudocode for generating pseudorandom numbers.

1. RandInt(): takes no inputs and returns a pseudorandom integer from the range of all possible integers that the language can store in memory.
2. RandIntn(): takes as input a non-negative integer n and returns a pseudorandom integer between 0 and n – 1, inclusively.
3. RandFloat(): takes no inputs and returns a pseudorandom decimal number in the range [0, 1).

We can access Go’s versions of these three functions using the respective function calls rand.Int(), rand.Intn(), and rand.Float64(). Let’s print the result of each of these functions on sample inputs, which will require us to import the "math/rand" package.

package main

import (
    "fmt"
    "math/rand"
)

func main() {
    fmt.Println("Rolling dice.")

    fmt.Println(rand.Int()) // prints integer 
    fmt.Println(rand.Intn(10)) // prints integer between 0 and 9, inclusively
    fmt.Println(rand.Float64()) // prints decimal in range [0, 1)
}

Let’s run our code multiple times by executing our code multiple times. There is no need to compile our code again since it hasn’t changed, so re-execute the terminal commands ./dice (on MacOS) or dice.exe (on Windows). As you might expect, we obtain different results each time the code is run.

Seeding Go’s PRNG

Yet for many years, regardless of the computer or operating system, the above code would always produce the same three numbers. To understand why, we recall a fact that we learned when we first introduced PRNGs.

As we learned in the core text, any pseudorandom number generator (PRNG) follows a process that is not truly random. As a result, Go’s PRNG must be initialized with some value, called the seed of the PRNG. We can change this seed ourselves by invoking the function rand.Seed(), which takes an integer as input and returns no outputs. Let’s add a call to rand.Seed() to func main(), before we ever generate any random numbers.

func main() {
    fmt.Println("Rolling dice.")

    rand.Seed(1) // seeding PRNG with an arbitrary value.

    fmt.Println(rand.Int()) // prints integer 
    fmt.Println(rand.Intn(10)) // prints integer between 0 and 9, inclusively
    fmt.Println(rand.Float64()) // prints decimal in range [0, 1)
}

Regardless of how many times this code is run, we obtain the same sequence of three numbers: 5577006791947779410, 7, and 0.6645600532184904. In fact, for the first fifteen years of Go’s existence, these are the three numbers that we would obtain if we didn’t have the rand.Seed() function call. This is because, behind the scenes, Go would automatically call rand.Seed(1). So what changed?

Starting with Go version 1.20, Go began automatically seeding its built-in PRNG based on the current time. We could do this ourselves using the following code that requires importing the "time" package, but this code is not necessary, and we will remove it going forward in this code along.

func main() {
    fmt.Println("Rolling dice.")

    rand.Seed(time.Now().UnixNano()) //seed PRNG based on time; this line is not necessary!

    fmt.Println(rand.Int()) // prints integer 
    fmt.Println(rand.Intn(10)) // prints integer between 0 and 9, inclusively
    fmt.Println(rand.Float64()) // prints decimal in range [0, 1)
}

Rolling a single die

We are now ready to implement RollDie(). We can generate a pseudorandom integer between 0 and 5, inclusively, using the function rand.Intn(6); we then add 1 to the resulting number.

//RollDie takes no inputs and returns a pseudorandom integer between 1 and 6, inclusively.
func RollDie() int {
    return rand.Intn(6) + 1
}

Rolling two (or multiple) dice

As we mentioned in the core text, one way of simulating the roll of two dice is to consult a table telling us how many of the 36 possibilities for the values on two dice correspond to each possible value of the sum (figure reproduced below). This table tells us that the two dice sum to 2 with probability 1/36, sum to 3 with probability 2/36, sum to 4 with probability 3/36, and so on.

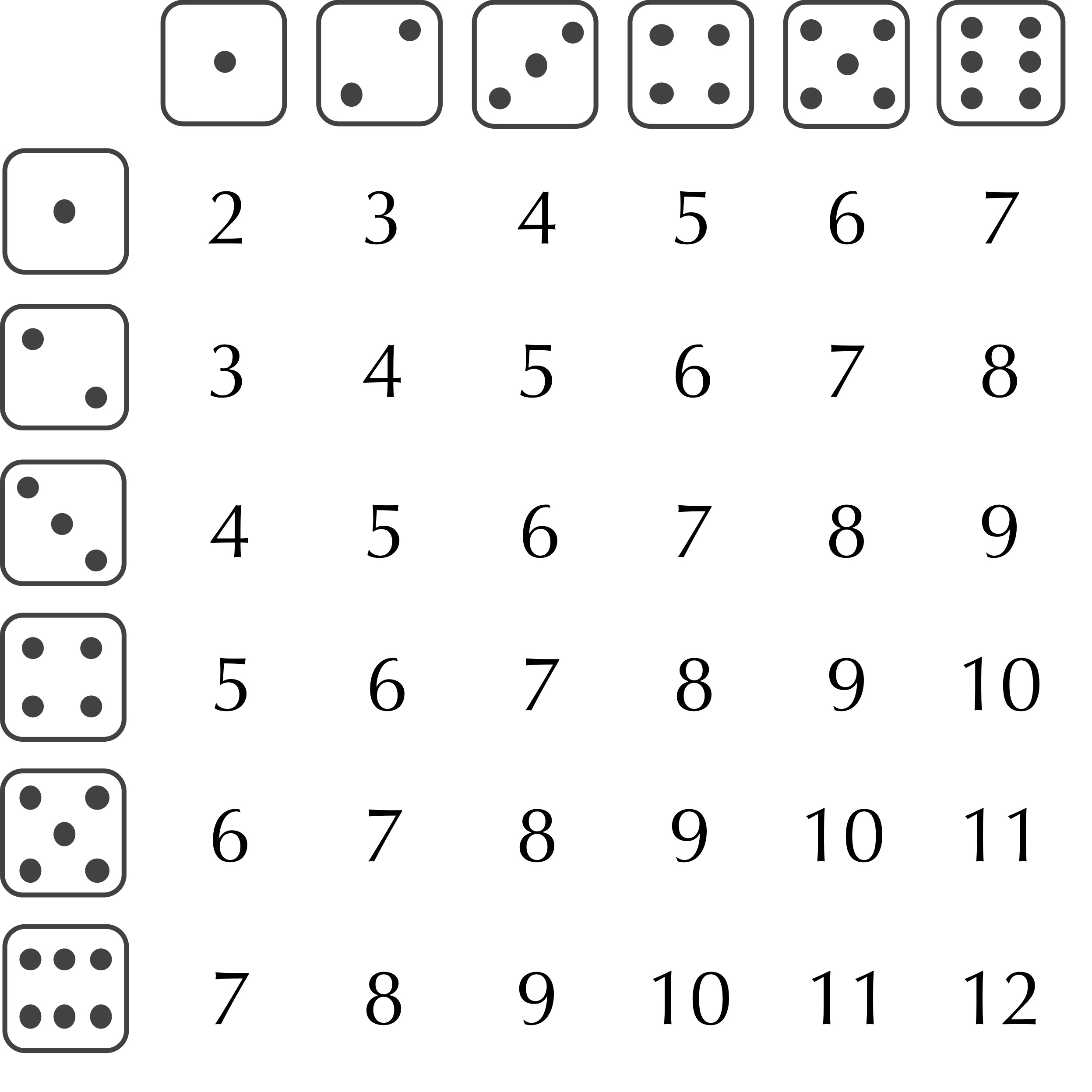
When faced with a problem in which a collection of events have probabilities summing to 1, we can simulate choosing one of these events by dividing the number line between 0 and 1 into segments whose lengths correspond to the probabilities. We can then generate a random number between 0 and 1, and assign an event based on the segment to which this number is assigned. In this particular case, a number between 0 and 1/36 would be assigned a dice roll summing to 2, a number between 1/36 and 3/36 would be assigned a dice roll summing to 3, a number between 3/36 and 6/36 would be assigned a dice roll summing to 4, and so on, allowing us to write a SumTwoDice() function as follows.

//SumTwoDice takes no inputs.
//It returns the sum of two simulated fair six-sided dice.
func SumTwoDice() int {
    roll := rand.Float64()

    if roll < 1.0/36.0 {
        return 2
    } else if roll < 3.0/36.0 {
        return 3
    } else if roll < 6.0/36.0 {
        return 4
    }
    //etc.
}

Such an approach might have a certain finality, and yet imagine the ramifications of needing to add a third, fourth, or fifth die; we would find ourselves writing if statements forever.

Fortunately, we are studying computer science instead of mathematics, a domain in which laziness has long proven to be a virtue. In this case, to roll two dice, why not simply roll one die twice! As a result, our SumTwoDice() function can be written in a single line.

//SumTwoDice takes no inputs.
//It returns the sum of two simulated fair six-sided dice.
func SumTwoDice() int {
    return RollDie() + RollDie()
}

Better yet, our observation allows us to generalize our function to an arbitrary number of dice by adding an integer parameter numDice.

//SumDice takes as input an integer numDice.
//It returns the sum of numDice simulated fair six-sided dice.
func SumDice(numDice int) int {
    sum := 0

    for i := 0; i < numDice; i++ {
        sum += RollDie()
    }

    return sum
}

Check your work from the code along

We now provide autograders in the window below (or via a direct link) allowing you to check your work for the following functions:

• RollDie()
• SumDice()