Hidden Messages in the Replication Origin

Counting words

We will begin with our first problem and look for the hidden message that makes an ori region special.

Various biological processes involving DNA require proteins to bind to the DNA. For example, a transcription factor binds to a specific DNA sequence and initiates the process of transcribing the DNA template into RNA, which is then sent out of the cell nucleus and used to produce other proteins. Many DNA-binding proteins “read” the DNA and will only bind to DNA when they detect a specific “keyword”, i.e., DNA string.

The more occurrences of the nucleotide string in the desired location of the genome, the more likely that binding will successfully occur (and the less likely that a mutation will disrupt the binding process). Therefore, a bacterium will most likely have evolved to have multiple occurrences of the nucleotide string in the region of the genome where a given protein binds with DNA. This is but one more illustration of the famous Theodore Dobzhansky quote, “Nothing in biology makes sense except in the light of evolution.”

In the case of replication, we know that replication initiation is mediated by DnaA, a protein that binds to a short segment within the ori known as a DnaA box. Let’s see, then, if we can find any surprisingly frequent “words” within the ori of Vibrio cholerae that might be DnaA boxes. First, we will consider the problem of counting the number of occurrences of a given pattern in a text. If a string appears within a longer text, we say that it is a substring of the text. This brings us to the following computational problem.

We will account for overlapping occurrences of pattern in text. For example, we will say that "ATA" occurs three times in "CGATATATCCATAG", not twice.

Our plan is to “slide a window” down text, checking whether each length-k substring of text matches pattern, and adding one to a count variable every time we encounter a match (see figure below). It is just a matter of converting this idea into a pseudocode function PatternCount() solving the Substring Counting Problem.

Continuing the use of 0-based indexing from Chapter 0, we might think of a string as similar to an array of symbols, so that text begins at position 0 and ends at position length(text)−1, where length(text) denotes the number of symbols in text.

The notation that many programming languages use for the length-k substring of text starting at position i of text is text[i, i + k]. For example, if text is "GACCATACTG", then text[2, 8] is "CCATAC", and text[4, 6] is "AT". This notation is convenient for two reasons. First, note that the length of the substring text[i, j] is always equal to j – i, and so we will immediately know that text[2, 8] has length equal to 8–2 = 6. Second, we can always infer the final index of the substring in text by subtracting 1 from the higher index. That is, the string text[2, 8] is the substring of text that begins at position 2 and ends at position 7.

Before continuing, we also note that the same notation applies to subarrays, or contiguous arrays inside arrays. If a is an array, then a[i, j] is the subarray of a of length j – i that starts at index i and continues up to and not including index j.

On the heels of the preceding exercise, note that the starting positions of substrings of text having length k range from 0 up to and including length(text) − k. For example, the last 3-mer of "GACCATACTG" starts at position 10 − 3 = 7. This discussion results in our desired pseudocode function solving the Substring Counting Problem.

PatternCount(pattern, text)
    count ← 0
    n ← length(text)
    k ← length(pattern)
    for every integer i between 0 and n − k
        if text[i, i + k] = pattern
            count ← count + 1
    return count

The Frequent Words Problem

Now that we can count the number of times that a given pattern appears in a longer string, we will return to our original problem of finding patterns that occur frequently.

We will apply the term k-mer as shorthand to refer to a string of length k. We say that pattern is a most frequent k-mer in text if it occurs in text at least as often as any other k-mer. You can verify that "ACTAT" is a most frequent 5-mer for "ACAACTATGCATACTATCGGGAACTATCCT", and that "ATA" is a most frequent 3-mer for "CGATATATCCATAG".

We now have a rigorously defined computational problem. Before continuing, you might like to brainstorm how we can solve it using an array. What subroutines might be useful?

Many algorithms will solve the frequent words problem. For example, we might try to generate all possible k-mers, and generate an array whose i-th value is the number of occurrences of the i-th k-mer. This approach is likely inefficient unless k is very small because the number of possible k-mers grows very quickly in terms of k (how many k-mers can you form from the DNA alphabet {A, C, G, T})?

Another array-based approach proceeds as follows.

1. Create an array count of length length(text)-k+1.
2. For each i, set count[i] equal to the number of times text[i, i+k] appears in text.
3. Consider the maximum values of count[i]. For any i achieving this maximum, the substring text[i, i + k] is a frequent k-mer.

For example, the array count for text ="ACGTTTCACGTTTTACGG" and k = 3 is shown in the figure below. Note that the maximum value is achieved six times at the indices 0, 3, 7, 10, 11, and 14. The indices 0, 7, and 14 correspond to the three starting positions of "ACG", and the indices 3, 10, and 11 correspond to the three starting positions of "TTT".

Once we have generated the count array of text, we know that the most frequent k-mers in text will be those whose corresponding entries in count are the largest. We should first write a function to find the maximum value of an array.

We are nearly ready to write pseudocode for a function FrequentWords() solving the Frequent Words Problem. This function will leverage the idea from ListPrimes() in Chapter 0 of forming an empty array freqPatterns to which we will add any frequent words that we find. However, note that when we range through count, we will encounter multiple indices in the array corresponding to the same substring (recall that indices 0, 7, and 14 all correspond to "ACG" in the above example). As a result, we should only append a string text[i, i+k] to freqPatterns if it is not already present in freqPatterns. This discussion motivates the following exercise.

We are now ready to present the function FrequentWords() that implements our array-based idea for finding frequent k-mers in a string.

FrequentWords(text, k)
    freqPatterns ← an array of strings of length 0
    n ← length(text)
    count ← an array of integers of length n − k + 1
    for every integer i between 0 and n − k
        pattern ← text[i, i + k]
        count[i] ← PatternCount(text, pattern)
    max ← MaxArray(count)
    for every integer i between 0 and n − k
        if count[i] = max
            pattern ← text[i, i + k]
            if Contains(freqPatterns, pattern) = false
                freqPatterns ← append(freqPatterns, pattern)
    return frequentPatterns

A faster frequent words approach

If you were to solve the Frequent Words Problem by hand for a small example, you would probably form a table like the one in the figure below for text equal to "ACGTTTCACGTTTTACGG" and k equal to 3. You would slide a length-k window text, and if the current k-mer substring of text does not occur in the table, then you would create a new entry for it. Otherwise, you would add 1 to the entry corresponding to the current k-mer substring of text. We call this table the frequency table for text and k.

In the previous FrequentWords() algorithm, we also make a single pass down text, but each time we encounter a k-mer window, we call the PatternCount() subroutine, which requires its own pass down the entire length of text. But when we build a frequency table, we make one pass down text, and every time we encounter a k-mer, we simply add 1 to the k-mer’s count.

We know that an array of length n is an ordered table of values, where we access the values using the integer indices 0 through n – 1. The frequency table is a generalized version of an array called a map or dictionary for which the indices are allowed to be arbitrary values (in this case, they are strings). More precisely, the indices of a map are called keys.

Given a map dict, we can access the value associated with a key key using the notation dict[key]. In the case of a frequency table called freq, we can access the value associated with some key string pattern using the notation freq[pattern]. The following pseudocode function takes a string text and an integer k as input and returns their frequency table as a map of string keys to integer values.

FrequencyTable(text, k)
    freqMap ← empty map
    n ← length(text)
    for every integer i between 0 and n − k
        pattern ← text[i, i + k]
        if freqMap[pattern] doesn't exist
            freqMap[pattern] = 1
        else
            freqMap[pattern]++
    return freqMap

Once we have built the frequency table, we can find all frequent k-mers if we determine the maximum value in the table, and then identify the keys of the frequency table achieving this value, appending each one that we find to a growing list. We are now ready to write a function BetterFrequentWords() to solve the Frequent Words Problem.

BetterFrequentWords(text, k)
    frequentPatterns ← an array of strings of length 0
    freqMap ← FrequencyTable(text, k)
    max ← MaxMap(freqMap)
    for all strings pattern in freqMap
        if freqMap[pattern] = max
            frequentPatterns ← append(frequentPatterns, pattern)
    return frequentPatterns

A remark on MaxMap() is in order. It would be very easy for us to imagine this as a straightforward function ranging over all the keys in the dictionary and updating a maximum variable m every time we find a bigger element. The following function implements this idea.

MaxMap(dict)
    m ← 0
    for every key pattern in dict
        if dict[pattern] > m
            m ← dict[pattern]
    return m

Yet we could imagine a map with string keys whose integer values are all negative. For such a map, we would set m equal to 0, and this value would never get updated because dict[pattern] would never be larger than m. As a result, we would erroneously return 0, rather than the true maximum value of the map.

Unlike with arrays, there is no particular order to how the keys of a map are ordered. We can nevertheless resolve the issue if we introduce a Boolean variable firstTime that will be true if we have not yet considered any of the keys of the map and will be set to false as soon as we consider the first key in the map.

MaxMap(dict)
    m ← 0
    firstTime = true
    for every key pattern in dict
        if firstTime = true or dict[pattern] > m
            firstTime= false
            m ← dict[pattern]
    return m

Frequent words in Vibrio cholerae

The figure below reveals the most frequent k-mers in the ori region from Vibrio cholerae. Do any of the counts seem surprisingly large?

For example, the 9-mer "ATGATCAAG" appears three times in the ori region of Vibrio cholerae — is it surprising?

atcaatgatcaacgtaagcttctaagcATGATCAAGgtgctcacacagtttatccacaacctgagtggatgacatcaagataggtcgttgtatctccttcctctcgtactctcatgaccacggaaagATGATCAAGagaggatgatttcttggccatatcgcaatgaatacttgtgacttgtgcttccaattgacatcttcagcgccatattgcgctggccaaggtgacggagcgggattacgaaagcatgatcatggctgttgttctgtttatcttgttttgactgagacttgttaggatagacggtttttcatcactgactagccaaagccttactctgcctgacatcgaccgtaaattgataatgaatttacatgcttccgcgacgatttacctcttgatcatcgatccgattgaagatcttcaattgttaattctcttgcctcgactcatagccatgatgagctcttgatcatgtttccttaaccctctattttttacggaagaATGATCAAGctgctgctcttgatcatcgtttc

We highlight a most frequent 9-mer instead of using some other value of k because experiments have revealed that bacterial DnaA boxes are usually nine nucleotides long. The probability that there exists a 9-mer appearing three or more times in a randomly generated DNA string of length 500 is approximately 1/1300. In fact, there are four different 9-mers repeated three or more times in this region: "ATGATCAAG", "CTTGATCAT", "TCTTGATCA“, and "CTCTTGATC".

The low likelihood of witnessing even one repeated 9-mer in the ori region of Vibrio cholerae leads us to the working hypothesis that one of these four 9-mers may represent a potential DnaA box that, when appearing multiple times in a short region, jump-starts replication. But which one?

Complementary DNA strands run in opposite directions

Recall that nucleotides A and T are complements of each other, as are C and G. The figure below shows a template strand "AGTCGCATAGT" and its complementary strand "ACTATGCGACT".

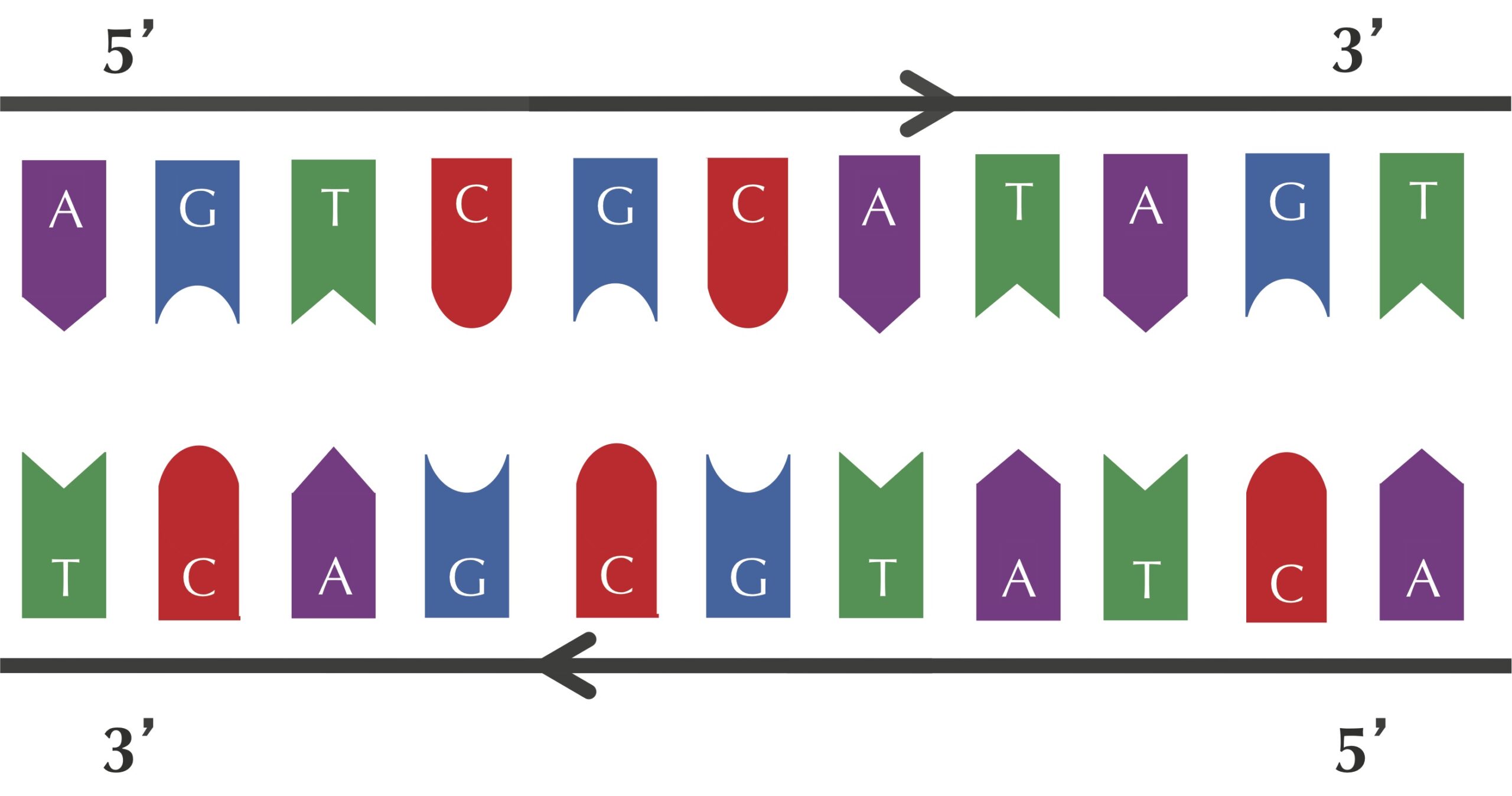
At this point, you may think that we have made a mistake, since the complementary strand in this figure reads out "TCAGCGTATCAT" from left to right rather than "ACTATGCGACT". We have not: each DNA strand has a direction (strands are read in the direction from 5′ to 3′), and the complementary strand runs in the opposite direction to the template strand, as shown by the arrows in the figure above.

Reverse complementing a string and the power of modularity

The reverse complement of a string pattern is the string formed by taking the complement of each nucleotide in pattern, then reversing the resulting string. The following problem is fundamental in computational biology.

We could write a single function solving the Reverse Complement Problem, but we can instead pass our work to two subroutines. Reverse() will return the reverse of an input string, whereas Complement() will take the string formed by complementing each nucleotide in a DNA string (but not reversing the string).

ReverseComplement(pattern)
    pattern ← Reverse(pattern)
    pattern ← Complement(pattern)
    return pattern

This function offers an example of the power of modularity, or dividing code into small functions that call each other. Modular code is easier to write, easier to read, and easier to debug, since we can test functions independently of each other to diagnose issues. In this case, we will first note the following shorter version of the ReverseComplement() function.

ReverseComplement(pattern)
    return Reverse(Complement(pattern))

Interestingly, among the four most frequent 9-mers in the ori region of Vibrio cholerae, "ATGATCAAG" and "CTTGATCAT" are reverse complements of each other, resulting in the following six occurrences of these strings.

atcaatgatcaacgtaagcttctaagcATGATCAAGgtgctcacacagtttatccacaacctgagtggatgacatcaagataggtcgttgtatctccttcctctcgtactctcatgaccacggaaagATGATCAAGagaggatgatttcttggccatatcgcaatgaatacttgtgacttgtgcttccaattgacatcttcagcgccatattgcgctggccaaggtgacggagcgggattacgaaagcatgatcatggctgttgttctgtttatcttgttttgactgagacttgttaggatagacggtttttcatcactgactagccaaagccttactctgcctgacatcgaccgtaaattgataatgaatttacatgcttccgcgacgatttacctCTTGATCATcgatccgattgaagatcttcaattgttaattctcttgcctcgactcatagccatgatgagctCTTGATCATgtttccttaaccctctattttttacggaagaATGATCAAGctgctgctCTTGATCATcgtttc

We should note that we don’t know whether "ATGATCAAG" or "CTTGATCAT" is the true “message” to which DnaA binds. If the message is "ATGATCAAG", then every occurrence of "CTTGATCAT" above is an occurrence of "ATGATCAAG" on the complementary strand of DNA. If the message is "CTTGATCAT", then every occurrence of "ATGATCAAG" above will appear as "CTTGATCAT" in the complementary strand. DnaA is not able to tell the difference between the two strands of DNA, and so it will see six occurrences of its hidden message.

Finding a 9-mer that appears six times (either as itself or as its reverse complement) in a DNA string of length 500 is far more surprising than finding a 9-mer that appears three times (as itself). This observation leads us to the working hypothesis that "ATGATCAAG" and its reverse complement "CTTGATCAT" represent a DnaA box in Vibrio cholerae.

The Pattern Matching Problem

However, before concluding that we have found the DnaA box of Vibrio cholerae, the careful bioinformatician should check if there are other short regions in the Vibrio cholerae genome exhibiting multiple occurrences of "ATGATCAAG" or "CTTGATCAT". After all, maybe these strings occur as repeats throughout the entire Vibrio cholerae genome, rather than just in the ori region. To this end, we should solve the following computational problem.

Note how similar this problem is to the Counting Words Problem. Here, rather than counting the number of occurrences of a pattern within a longer string, we are finding all the starting positions of this pattern within the string. Our function, which we call StartingIndices(), should therefore range over all the k-mers of text and append any k-mers that match pattern to a growing list, which we call positions.

StartingIndices(pattern, text)
    positions ← array of integers of length 0
    n ← length(text)
    k ← length(pattern)
    for every integer i between 0 and n − k
        if text[i, i + k] = pattern
            positions ← append(positions, i)
    return positions

There is a general programming principle at hand. Any time we write code that is very similar to what we have already written, we should be wary that we can use a subroutine instead. In this case, note that once we have the array positions storing the starting indices of all occurrences of pattern in text, we can obtain the number of pattern matches just by accessing the length of positions. As a result, we can rewrite the PatternCount() function using StartingIndices() as a subroutine and obtain a shorter function leveraging modularity.

PatternCount(pattern, text)
    positions ← StartingIndices(pattern, text)
    return length(positions)

After implementing the Pattern Matching Problem, we discover that "ATGATCAAG" appears 17 times in the following positions of the Vibrio cholerae genome:

116556, 149355, 151913, 152013, 152394, 186189, 194276, 200076, 224527, 307692, 479770, 610980, 653338, 679985, 768828, 878903, 985368

With the exception of the highlighted three occurrences of "ATGATCAAG" in ori at starting positions 151913, 152013, and 152394, no other instances of "ATGATCAAG" form clumps, i.e., appear close to each other in a small region of the genome. You may check that the same conclusion is reached when searching for "CTTGATCAT". We now have strong statistical evidence that "ATGATCAAG" and "CTTGATCAT" may represent the hidden message to DnaA to start replication.