Implementing the Game of Life in Go

Learning objectives

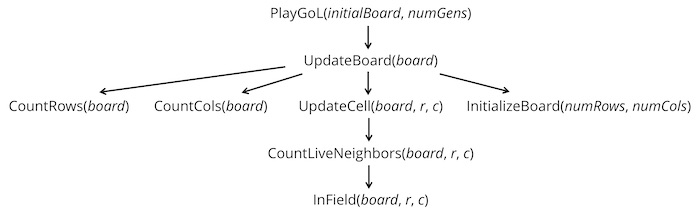
In this code along, we will implement the engine of the Game of Life corresponding to the function hierarchy for the Game of Life (reproduced below) that we encountered when we discussed the Game of Life in the core text. We will then use the code that we wrote in the previous code along to visualize a Game of Life board in order to animate the automaton over multiple generations and see the beautiful behavior that results.

Along the way, we will also learn how to parse parameters from the command line that we can pass to the functions that we write, and apply this idea to our Game of Life program.

Setup

This code along will build upon the starter code that we expanded in the previous code along. In particular, we will be working with the gameOfLife folder, which has the following structure:

boards: a directory containing .csv files that represent different initial Game of Life board states (more on this directory shortly).
output: an initially empty directory that will contain images and GIFs that we draw.
datatypes.go: a file that will contain type declarations (more to come shortly).
functions.go: a file that will contain functions that we will write in the next code along for implementing the Game of Life.
io.go: a file that will contain code for reading in a Game of Life board from file.
main.go: a file that will contain func main(), where we will call functions to read in Game of Life boards and then draw them.

We will be editing functions.go in this code along; at the end of the code along, we will write some code in main.go, so make sure that func main() does not have any code. Here is what our own func main() contains.

func main() {
	fmt.Println("Coding the Game of Life!")
}

Code along summary

Our highest level function: playing the Game of Life

We will first focus on our highest level function, PlayGameOfLife(). This function takes as input an initial GameBoard object initialBoard as well as an integer parameter numGens indicating the number of generations in our simulation. It creates a slice of numGens+1 total GameBoard objects, sets the first one equal to initialBoard, and then progressively sets boards[i] by updating the previous board boards[i-1] according to the rules of the Game of Life.

As we will see throughout this course, although PlayGameOfLife() achieves something amazing, the function is quite short, passing most of the heavy lifting to a subroutine UpdateBoard() that takes a GameBoard object as input and returns the GameBoard resulting from applying the Game of Life rules to the input board over a single generation.

// PlayGameOfLife takes as input an initial game board and a number of generations.
// It returns a slice of game boards of length numGens+1 corresponding to playing
// the Game of Life over numGens generations, starting with the initial board.
func PlayGameOfLife(initialBoard GameBoard, numGens int) []GameBoard {
	boards := make([]GameBoard, numGens+1)
	boards[0] = initialBoard

	for i := 1; i <= numGens; i++ {
		boards[i] = UpdateBoard(boards[i-1])
	}

	return boards
}

Note: Recall that although we plan to visualize an animation of the Game of Life later, we are not yet drawing any of the GameBoard objects to images, but rather storing all of the boards along the way as two-dimensional boolean slices.

Updating a single generation of the Game of Life

We next turn to implementing UpdateBoard(). As the function hierarchy indicates, UpdateBoard() relies on four subroutines, the first two of which we wrote at the end of the previous code along.

CountRows(): takes as input a GameBoard and returns the number of rows in the board.
CountColumns(): takes as input a GameBoard and returns the number of columns in the board.
InitializeBoard(): takes as input integers numRows and numCols and creates a rectangular GameBoard in which all values are set to the default value of false.
UpdateCell(): takes as input a GameBoard object as well as integers r and c, and returns a boolean value corresponding to the state of the element of the GameBoard at row r and column c in the next generation of the Game of Life.

We first call CountRows() and CountColumns() to determine the number of rows and columns of the current GameBoard. Then, we initialize a GameBoard called newBoard to have these same dimensions; we will eventually return newBoard.

// UpdateBoard takes as input a GameBoard.
// It returns the board resulting from playing the Game of Life for one generation.
func UpdateBoard(currentBoard GameBoard) GameBoard {
	// first, create new board corresponding to the next generation.
	numRows := CountRows(currentBoard)
	numCols := CountColumns(currentBoard)
	newBoard := InitializeBoard(numRows, numCols)

	// to fill in

	return newBoard
}

We then use a nested for loop to range over all the cells in the current board and update the cells of newBoard. We pass currentBoard along with the row and column indices into a subroutine UpdateCell(), which returns the updated state of this cell in the next generation (as a boolean value). We then set newBoard[r][c] equal to this updated state.

// UpdateBoard takes as input a GameBoard.
// It returns the board resulting from playing the Game of Life for one generation.
func UpdateBoard(currentBoard GameBoard) GameBoard {
	// first, create new board corresponding to the next generation.
	numRows := CountRows(currentBoard)
	numCols := CountColumns(currentBoard)
	newBoard := InitializeBoard(numRows, numCols)

	//range through all cells of currentBoard and update each one into newBoard.
	for r := range currentBoard {
		// range over values in currentBoard[r], the current row
		for c := range currentBoard[r] {
			//curr value is currentBoard[r][c]
			newBoard[r][c] = UpdateCell(currentBoard, r, c)
		}
	}

	return newBoard
}

Updating a single cell of a Game of Life board

We now will write the two remaining subroutines InitializeBoard() and UpdateCell(), starting with the former, which is just a matter of making a GameBoard with default false values having the given number of rows and columns. Now that we are getting comfortable working with two-dimensional arrays, this task may start to feel easy.

// InitializeBoard takes as input a number of rows and a number of columns.
// It returns a numRows x numCols GameBoard object.
func InitializeBoard(numRows, numCols int) GameBoard {
	b := make(GameBoard, numRows)
	for i := range b {
		b[i] = make([]bool, numCols)
	}

	return b
}

We can then turn to implementing UpdateCell(), which determines the state of a cell in the next generation of the Game of Life. To do so, it first uses a subroutine to count the number of live neighbors of board[r][c], and it then applies the appropriate rule of the Game of Life based on the number of live neighbors as well as whether the cell at board[r][c] is alive. For convenience, the Game of Life rules are reproduced below.

A (Propagation): If a cell is alive and has either two or three live neighbors, then it remains alive.

B (Lack of mates): If a cell is alive and has zero or one live neighbors, then it dies out.

C (Overpopulation): If a cell is alive and has four or more live neighbors, then it dies out.

D (Rest in peace): If a cell is dead and has more than or fewer than three live neighbors, then it remains dead.

E (Zombie): If a cell is dead and has exactly three live neighbors, then it becomes alive.

UpdateCell() uses an if statement to determine if board[r][c] is alive. If so, then it considers the number of live neighbors to determine whether rule A applies, in which case we return true; otherwise, rule B or C applies, and we return false. If board[r][c] is dead, then we return true only if the number of live neighbors is 3 (rule D applies); otherwise, rule E applies, and we return false.

// UpdateCell takes a GameBoard and row/col indices r and c, and it returns the state of the board at these row/col indices is in the next generation.
func UpdateCell(board GameBoard, r, c int) bool {
	numNeighbors := CountLiveNeighbors(board, r, c)

	// now it's just a matter of consulting the rules.
	if board[r][c] == true { // I'm alive
		if numNeighbors == 2 || numNeighbors == 3 {
			return true // stayin alive
		} else {
			return false // dyin out
		}
	} else { //I'm ded
		if numNeighbors == 3 { //zombie!
			return true
		} else { // RIP
			return false
		}
	}
}

The nitty gritty: counting live neighbors of a cell

As we observed in the core text, the trickiest details are contained in the lowest levels of a function hierarchy. In particular, we should be careful when implementing CountLiveNeighbors(), which takes as input a GameBoard as well as integers r and c and returns the number of live neighbors in the 8-cell Moore neighborhood of board[r][c], which is reproduced in the figure below.

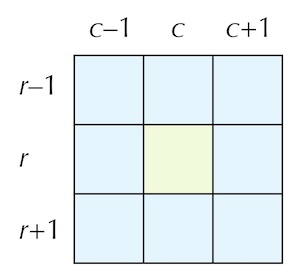
The Moore neighborhood of the cell at position (r, c) of a Game of Life board.

Starting our implementation of CountLiveNeighbors() by declaring an integer variable count that will hold the number of live neighbors of board[r][c], which we will later return. To range over the Moore neighborhood of board[r][c], we will use two nested for loops, with i (our row index) ranging between r-1 and r+1, and j (our column index) ranging between c-1 and c+1.

// CountLiveNeighbors takes as input a GameBoard board along with row and column indices r, c.
// It returns the sum of live neighbors of board[r][c],
// not including cells that fall off the boundaries of the board.
func CountLiveNeighbors(board GameBoard, r, c int) int {
	count := 0

	// range over all cells in the neighborhood
	for i := r - 1; i <= r+1; i++ {
		for j := c - 1; j <= c+1; j++ {
			// to fill in
		}
	}

	return count
}

We only want to include board[i][j] in the neighborhood of board[r][c] if both of the following events occur:

board[i][j] is not the same cell as board[r][c], which will happen when either i != r or j != c. We can therefore verify this with the test (i != r || j != c).
board[i][j]lies within the confines of board, which we will check using a subroutine InField() that returns true if board[i][j] is on the board, and false otherwise.

Because both of these statements must be true in order for board[i][j] to belong to the neighborhood, we will combine them using the and operator (&&). If both statements are true, then we will have a final nested if statement determining whether board[i][j] is true, in which case we will increment count by one.

// CountLiveNeighbors takes as input a GameBoard board along with row and column indices r, c.
// It returns the sum of live neighbors of board[r][c],
// not including cells that fall off the boundaries of the board.
func CountLiveNeighbors(board GameBoard, r, c int) int {
	count := 0

	// range over all cells in the neighborhood
	for i := r - 1; i <= r+1; i++ {
		for j := c - 1; j <= c+1; j++ {
			// only include cell (i, j) if it isn't (r, c) and is on the board
			if (i != r || j != c) && InField(board, i, j) {
				if board[i][j] == true {
					// we found a live one!
					count++
				}
			}
		}
	}

	return count
}

Note: We have previously noted that nested loops can sometimes be replaced by code that uses subroutines. In this particular case, it might prove confusing to parse out the most internal if statements as subroutines.

Checking if a cell is within the confines of the board

Finally, we have reached the bottom of the function hierarchy, where InField() is lurking. This function takes as input board as well as integers i and j. It returns true if the cell at position (i, j) is within the boundaries of board, and false otherwise.

To implement this function, we will instead check if (i, j) is outside the boundaries of board. This will occur if either i or j is negative, if i is greater than the number of rows in board, or if j is greater than the number of columns in board. If any of these is true, then InField() should return false; otherwise, it should return true.

We first check if i or j is negative by using the || connector.

// InField takes a GameBoard board as well as row and col indices (i, j).
// It returns true if board[i][j] is in the board and false otherwise.
func InField(board GameBoard, i, j int) bool {
	if i < 0 || j < 0 {
		return false
	}
        // to fill in
}

Next, we check if either i is greater than the number of rows in board, or if j is greater than the number of columns in board, again using the || connector.

// InField takes a GameBoard board as well as row and col indices (i, j).
// It returns true if board[i][j] is in the board and false otherwise.
func InField(board GameBoard, i, j int) bool {
	if i < 0 || j < 0 {
		return false
	}
	if i >= CountRows(board) || j >= CountColumns(board) {
		return false
	}
}

If we survive both of these checks, then we can conclude that (i, j) is within the boundaries of board, and we can safely return true as a default value.

// InField takes a GameBoard board as well as row and col indices (i, j).
// It returns true if board[i][j] is in the board and false otherwise.
func InField(board GameBoard, i, j int) bool {
	if i < 0 || j < 0 {
		return false
	}
	if i >= CountRows(board) || j >= CountColumns(board) {
		return false
	}
	// if we survive to here, then we are on the board
	return true
}

Taking command line arguments with os.Args

We are now ready to put some code into main.go to run our simulation. We will need four package imports: "fmt", "strconv", "os" (to process command line arguments), and "gifhelper" (to produce an animated GIF). As a result, main.go should initially look like the following.

package main

import (
	"fmt"
	"strconv"
	"os"
	"gifhelper"
)

func main() {
	fmt.Println("Coding the Game of Life!")
}

Until now, we have declared any parameters for running a simulation that we need within our code. The Game of Life offers us an opportunity to show a more advanced concept, which is allowing the user to change the parameters of the simulation themselves in the command line. Specifically, we will allow the user to change the following command line arguments at runtime.

The name of the file containing the initial Game of Life board.
The name of the file that will contain the final animated GIF that we draw.
The width (in pixels) of each square cell in our drawing.
The number of generations to run the simulation.

For example, we will eventually want to run our simulation in the following manner (executing gameOfLife.exe on Windows instead of ./gameOfLife):

./gameOfLife boards/rPentomino.csv output/rPentomino 20 1200

When code is run with command line arguments, behind the scenes, an array of strings is created called os.Args having length equal to one greater than the number of parameters given. The first element, os.Args[0], is always the name of the program. The remaining elements of os.Args are strings representing the parameters passed into the program. In this case, os.Args[1] is "gosperGun.csv", os.Args[2] is "gosperGun", os.Args[3] is "20", and os.Args[4] is "100". (You will now appreciate why we need to import the "strconv" package, since we will need to convert the last two parameters to integers.)

Let’s put this into practice in func main(). We will first read os.Args[1] as a variable initialBoardFile, which will be a string representing the file location of the initial board. Next, we will read in os.Args[2] as a variable outputFile, another string storing the location of the animated GIF that we will draw to visualize our simulation.

func main() {
	fmt.Println("Coding the Game of Life!")

	initialBoardFile := os.Args[1] // my starting GameBoard file name
	outputFile := os.Args[2]       // where to draw the final animated GIF of boards


	// to fill in
}

Next, we will read in the width of each cell in pixels and the number of generations as os.Args[3] and os.Args[4]. Before storing these values in the respective variables cellWidth and numGens, we need to use strconv.Atoi() to convert the arguments from strings to integers. Once we have done so, our work of reading parameters is finished, and so we will print a statement to the console to that effect.

func main() {
	fmt.Println("Coding the Game of Life!")

	initialBoardFile := os.Args[1] // my starting GameBoard file name
	outputFile := os.Args[2]       // where to draw the final animated GIF of boards

	// how many pixels wide should each cell be?
	cellWidth, err := strconv.Atoi(os.Args[3])
	if err != nil {
		panic("Error: Problem converting cell width parameter to an integer.")
	}

	// how many generations to play the automaton?
	numGens, err2 := strconv.Atoi(os.Args[4])
	if err2 != nil {
		panic("Error: Problem converting number of generations to an integer.")
	}

	fmt.Println("Parameters read in successfully!")

        //to fill in
}

Animating the Game of Life

Now that we have read in the command line arguments, we will take the following steps:

Read the Game of Life board from file by calling ReadBoardFromFile(initialBoardFile) and store the result in a GameBoard object called initialBoard.
Call PlayGameOfLife() on the parameters initialBoard and numGens to produce a slice of GameBoard objects boards corresponding to the generations of the simulation.
Generate a slice of images imglist by calling DrawGameBoards() on the two inputs boards and cellWidth.

We add code to implement these steps below. To save space, we are not showing the part of func main() devoted to processing command line arguments.

func main() {
	fmt.Println("Coding the Game of Life!")

	// command line argument processing ...

	initialBoard := ReadBoardFromFile(initialBoardFile)

	fmt.Println("Playing the automaton.")

	boards := PlayGameOfLife(initialBoard, numGens)

	fmt.Println("Game of Life played. Now, drawing images.")

	// we need a slice of image objects
	imglist := DrawGameBoards(boards, cellWidth)
	fmt.Println("Boards drawn to images! Now, convert to animated GIF.")
}

Now that we have a slice of image objects imglist from running the simulation, we just need to convert them to an animated GIF. To do so, we will use a function called ImagesToGIF() found in the gifhelper folder provided as starter code. This function takes as input a slice of image.Image objects imglist as well as a target file name (as a string). It returns no outputs, but it draws the images in imglist as an animated GIF to the file indicated in outputFile. (Recall that in this case, outputFile is equal to os.Args[2], the second command-line parameter.)

func main() {
	fmt.Println("Coding the Game of Life!")

	// command line argument processing ...

	initialBoard := ReadBoardFromFile(initialBoardFile)

	fmt.Println("Playing the automaton.")

	boards := PlayGameOfLife(initialBoard, numGens)

	fmt.Println("Game of Life played. Now, drawing images.")

	// we need a slice of image objects
	imglist := DrawGameBoards(boards, cellWidth)
	fmt.Println("Boards drawn to images! Now, convert to animated GIF.")

	// convert images to a GIF
	gifhelper.ImagesToGIF(imglist, outputFile)

	fmt.Println("Success! GIF produced.")
}

Running the simulation

We are now ready to run our simulation. Save, compile, and run the Game of Life code with the following terminal command (executing gameOfLife.exe on Windows instead of ./gameOfLife):

./gameOfLife boards/dinnerTable.csv output/dinnerTable 20 60

Executing this command produces the animated GIF shown below in our output folder.

The dinner table automaton oscillator with period 12.

Next, we will execute the following command to animate the R pentomino. We will keep cellWidth equal to 20, but we need to increase the number of generations to 1200 so that we can see the entire simulation. It will take a bit longer to complete, but the result will be worth it.

./gameOfLife boards/rPentomino.csv output/rPentomino 20 1200

The result is shown in the beautiful GIF below.

Finally, we will animate the Gosper glider gun using the following command:

./gameOfLife boards/gosperGun.csv output/gosperGun 20 400

The animation is shown below.

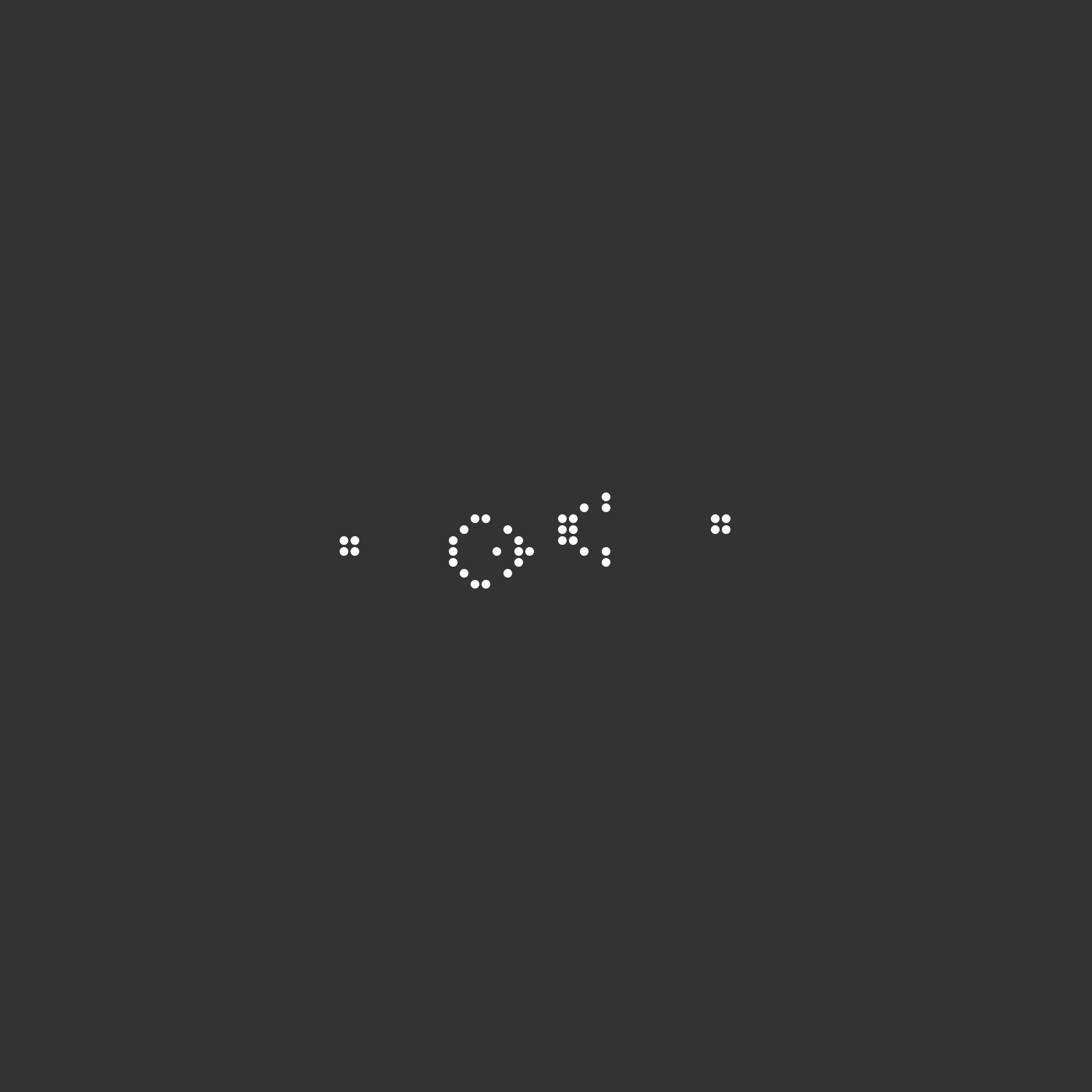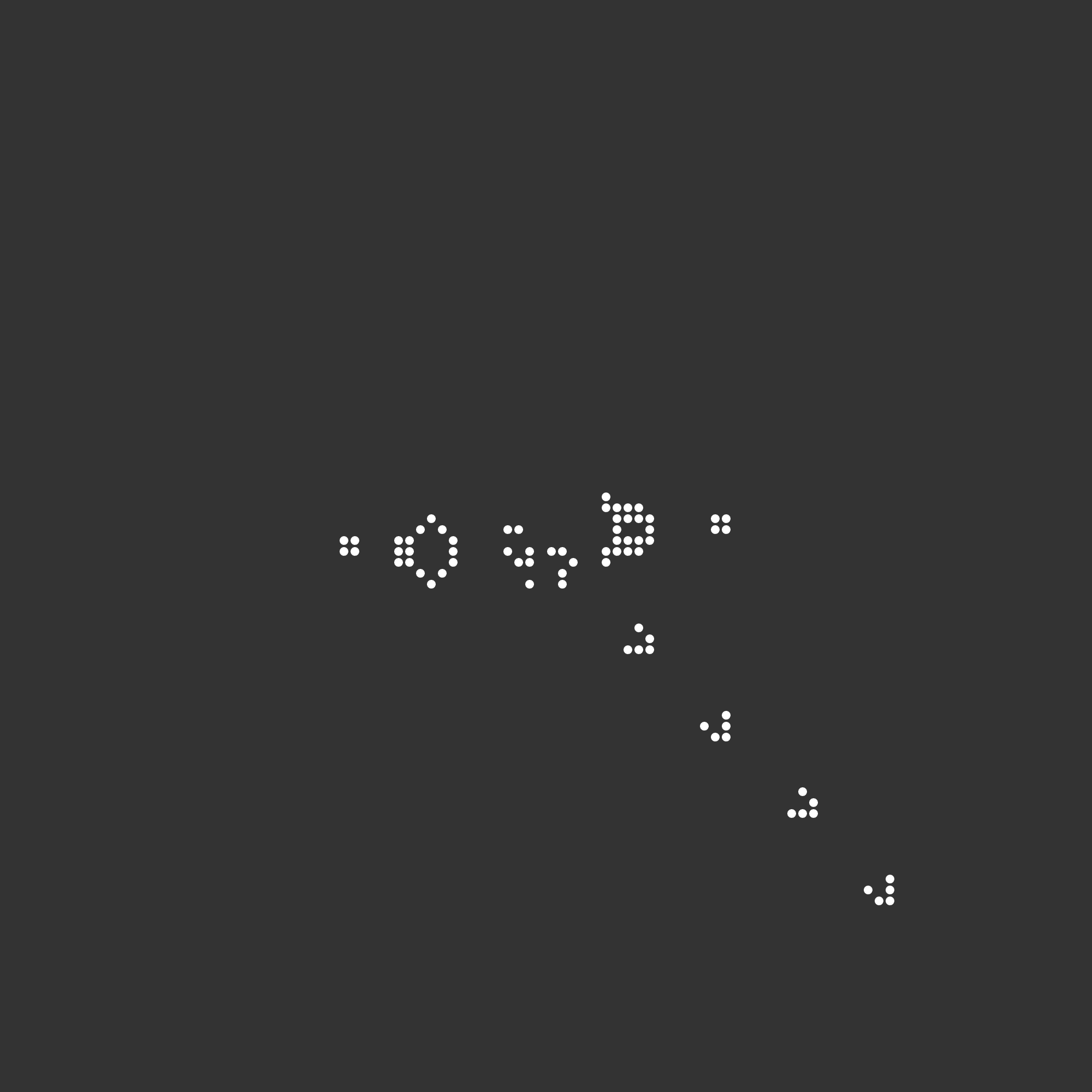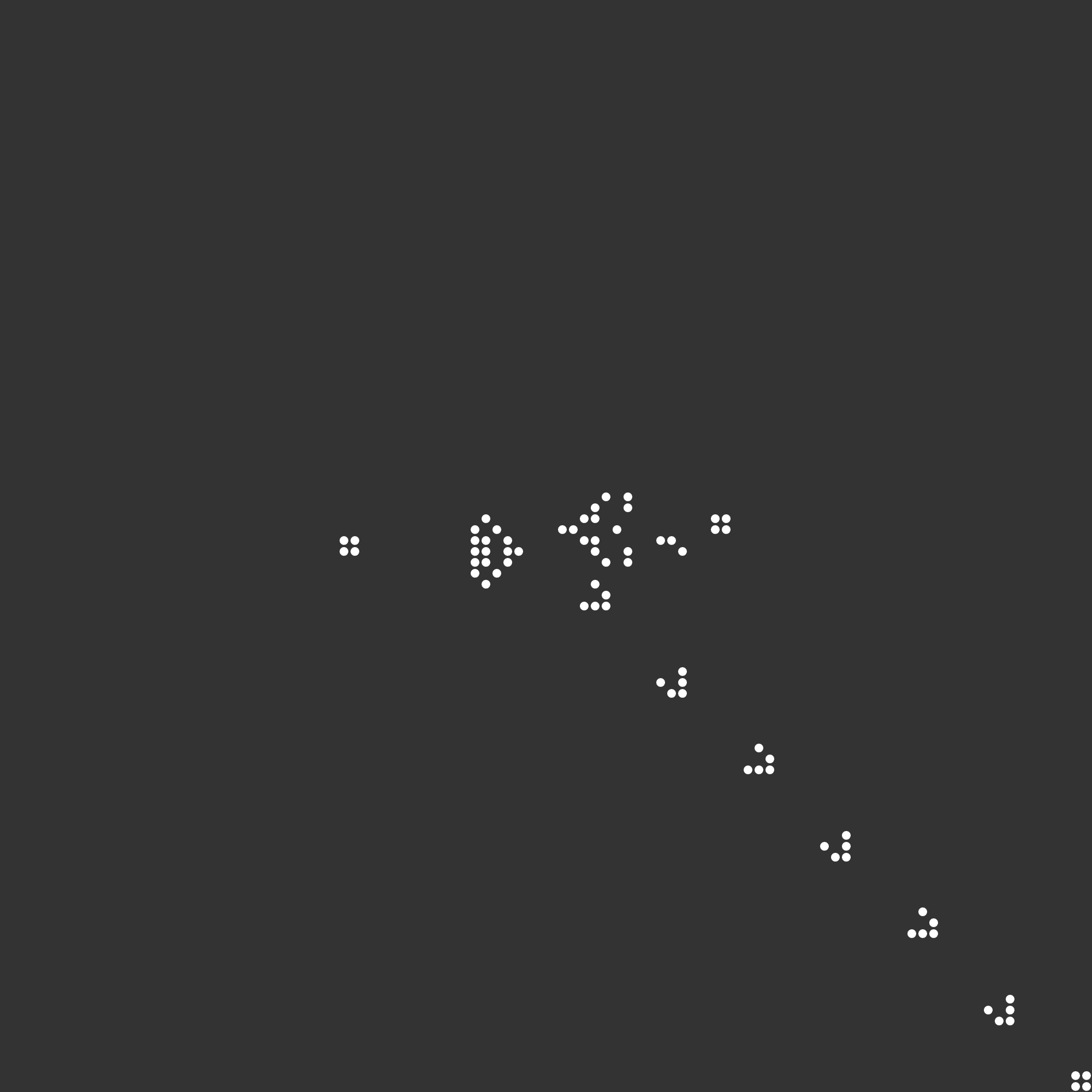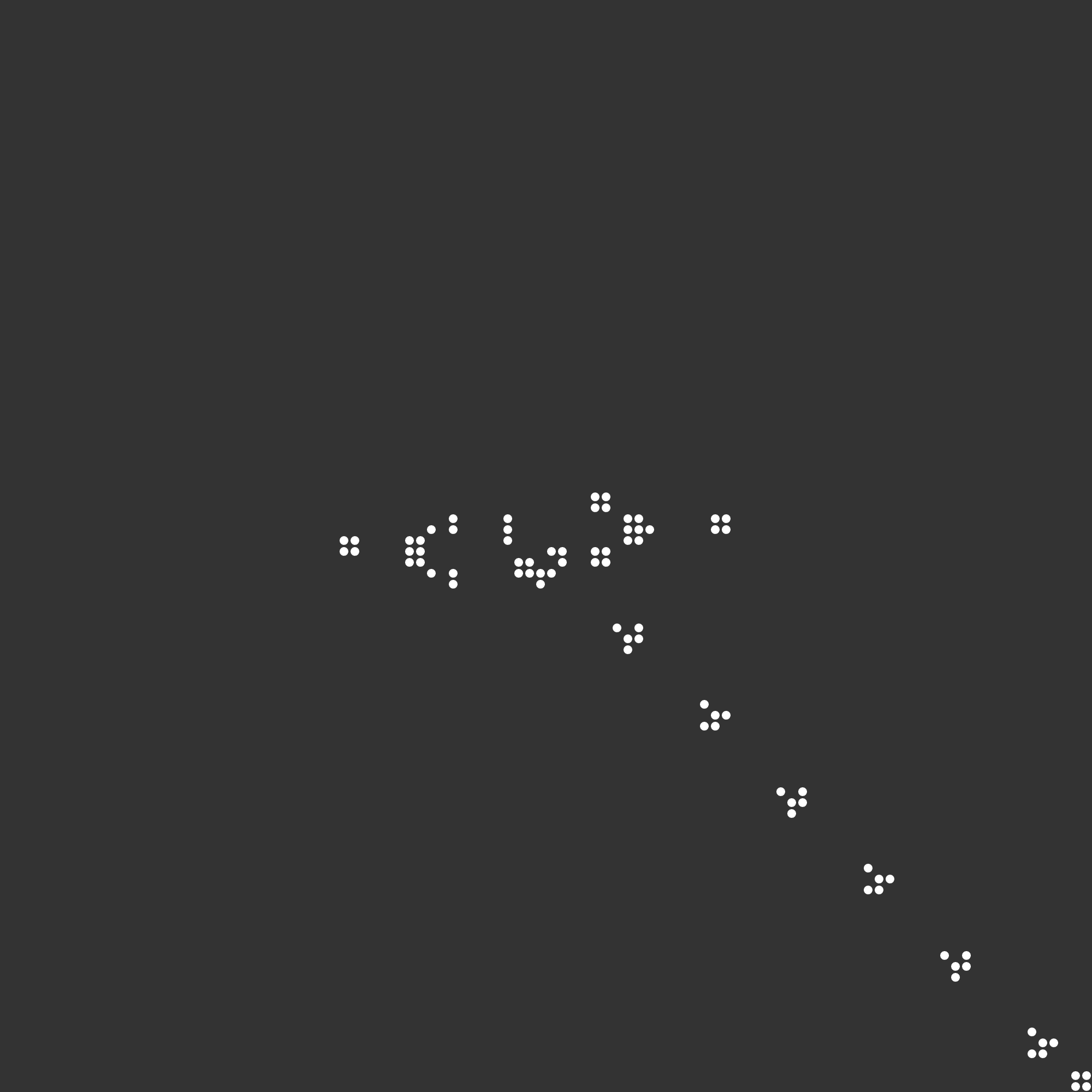
The Game of Life is undeniably beautiful. But our work is not done! In the next code along, we will turn our work toward implementing an arbitrary cellular automaton that can take any collection of rules. In particular, we will see one rule set called Langton’s loop that produces a self-replicating cellular automaton that will knock your socks off. Please join us, or check your work from this code along below.