Code along video
Beneath the video, we provide a detailed summary of the topics and code covered in the code along.
At the bottom of this page, you will have the opportunity to validate your work via auto-graded assessments that evaluate the functions covered in the code along.
Although we strongly suggest completing the code along on your own, you can find completed code from the code along in our course code repository.
Code along summary
We are now ready to return to our second main narrative in this chapter, finding prime numbers. In the preceding lesson, we saw that Euclid’s algorithm offers a substantial and surprising improvement over a trivial approach. How will the sieve of Eratosthenes fare against a simpler prime finding approach?
Below, we reproduce our pseudocode for TrivialPrimeFinder() and SieveOfEratosthenes() (along with necessary subroutines) from the main text.
TrivialPrimeFinder(n)
primeBooleans ← array of n+1 false boolean variables
for every integer p from 2 to n
if IsPrime(p) is true
primeBooleans[p] ← true
return primeBooleans
IsPrime(p)
for every integer k between 2 and √p
if k is a divisor of p
return false
return true
SieveOfEratosthenes(n)
primeBooleans ← array of n+1 true boolean variables
primeBooleans[0] ← false
primeBooleans[1] ← false
for every integer p between 2 and √n
if primeBooleans[p] = true
primeBooleans ← CrossOffMultiples(primeBooleans, p)
return primeBooleans
CrossOffMultiples(primeBooleans, p)
n ← length(primeBooleans) - 1
for every multiple k of p (from 2p to n)
primeBooleans[k] ← false
return primeBooleans
In this lesson, we will implement these two algorithms and time them.
Setup
Create a new folder called primes in your go/src directory, and then create a new file within the go/src/primes folder called main.go, which we will edit in this lesson.
In main.go, add the following starter code.
package main
import (
"fmt"
)
func main() {
fmt.Println("Finding primes.")
}
The trivial prime finding algorithm
We are now ready to return to TrivialPrimeFinder() and use what we have learned about slices in the previous code along. In the updated TrivialPrimeFinder() function below, we use a two-line declaration of the primeBooleans slice, but we could also use the single-line declaration primeBooleans := make([]bool, n+1).
//TrivialPrimeFinder takes an integer n and produces a boolean array of length n+1
//where primeBooleans[p] is true if p is prime (and false otherwise)
func TrivialPrimeFinder(n int) []bool {
var primeBooleans []bool // type is "slice of booleans", which default to false
primeBooleans = make([]bool, n+1)
// in general, you'll just use primeBooleans := make([]bool, n+1)
for p := 2; p <= n; p++ {
if IsPrime(p) == true {
primeBooleans[p] = true
}
}
return primeBooleans
}
We will need to implement IsPrime() as well. To do so, we will need to call the Sqrt() function from the "math" package. A first attempt at this function is below.
func IsPrime(p int) bool {
for k := 2; k <= math.Sqrt(p); k++ {
if p%k == 0 {
return false
}
}
return true
}
Unfortunately, this version of IsPrime() produces a compiler error because math.Sqrt() takes a float64 as input. To fix this issue, we will cast p to be a float64; we also will need to cast k when comparing it against the resulting square root.
func IsPrime(p int) bool {
for k := 2; float64(k) <= math.Sqrt(float64(p)); k++ {
if p%k == 0 {
return false
}
}
return true
}
Now that we have implemented IsPrime(), let’s now call TrivialPrimeFinder() from func main() and ensure that everything is working properly.
func main() {
fmt.Println("Primes and arrays.")
primeBooleans := TrivialPrimeFinder(10)
fmt.Println(primeBooleans)
}
STOP: Compile and runmain.go. You should seefalse false true true false true false true false false falseprinted to the console. This is correct becauseprimeBooleans[2],primeBooleans[3],primeBooleans[5], andprimeBooleans[7]should betrueto correspond to the primality of 2, 3, 5, and 7 (see figure below).
i | prime_booleans[i] |
| 0 | False |
| 1 | False |
| 2 | True |
| 3 | True |
| 4 | False |
| 5 | True |
| 6 | False |
| 7 | True |
| 8 | False |
| 9 | False |
| 10 | False |
prime_booleans[i] for an array of length 11.Implementing the sieve of Eratosthenes
We are now ready to implement the sieve of Eratosthenes. Below, we reproduce the pseudocode for SieveOfEratosthenes() as well as its subroutine CrossOffMultiples().
SieveOfEratosthenes(n)
primeBooleans ← array of n+1 true boolean variables
primeBooleans[0] ← false
primeBooleans[1] ← false
for every integer p between 2 and √n
if primeBooleans[p] = true
primeBooleans ← CrossOffMultiples(primeBooleans, p)
return primeBooleans
CrossOffMultiples(primeBooleans, p)
n ← length(primeBooleans) - 1
for every multiple k of p (from 2p to n)
primeBooleans[k] ← false
return primeBooleans
You may wish to recall how the sieve of Eratosthenes works, as illustrated in the figure below. It first assumes that every integer is prime. Then, over a sequence of steps, it identifies the smallest number in the table that is not composite, and then it “crosses off” all of that number’s factors larger than itself (i.e., sets them to be composite), which is the work of CrossOffMultiples().
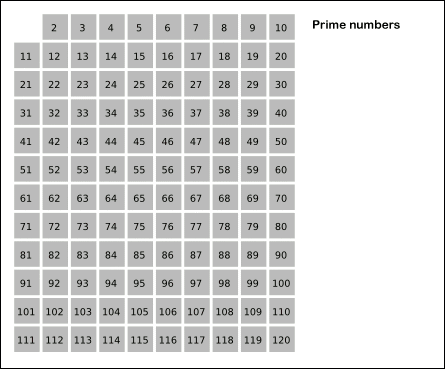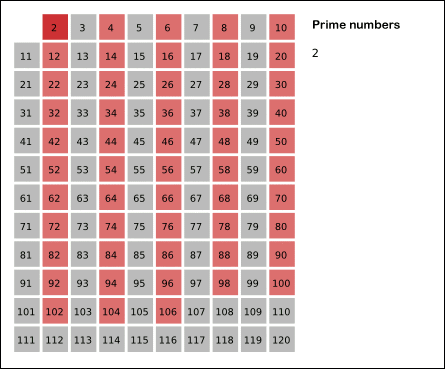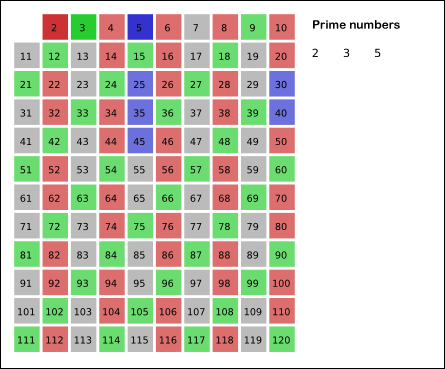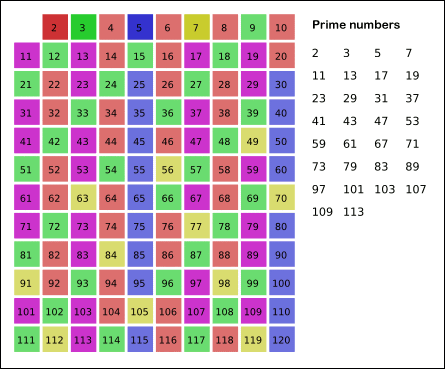
Like TrivialPrimeFinder(), we will need to declare primeBooleans as a slice of boolean variables. We know that this array will have length n+1, and so we can declare it to have this length. Let’s start writing our function below.
//SieveOfEratosthenes takes an integer n and returns a slice of n+1
//booleans primeBooleans where primeBooleans[p] is true if p is prime
//and false otherwise.
//It implements the sieve of Eratosthenes approach for finding primes.
func SieveOfEratosthenes(n int) []bool {
primeBooleans := make([]bool, n+1)
// the meat of our function will go here
return primeBooleans
}
When we declare primeBooleans, every value of this slice will be initialized with the default value of false. This default behavior is different to our desired initialization for the sieve of Eratosthenes, which is for every value other than primeBooleans[0] and primeBooleans[1] to be initialized to true. As a result, we first need a for loop setting all other values of primeBooleans to true.
//SieveOfEratosthenes takes an integer n and returns a slice of n+1
//booleans primeBooleans where primeBooleans[p] is true if p is prime
//and false otherwise.
//It implements the sieve of Eratosthenes approach for finding primes.
func SieveOfEratosthenes(n int) []bool {
primeBooleans := make([]bool, n+1)
// set everything to prime other than primeBooleans[0] and primeBooleans[1]
for k := 2; k <= n; k++ {
primeBooleans[k] = true
}
return primeBooleans
}
Next we are ready to implement the engine of the sieve. We use a for loop to range over all p between 2 and √n. Each time through the loop, we ask “Is p prime?” And if this is the case (i.e., if primeBooleans[p] is true), then we update our primeBooleans array by setting all indices of primeBooleans that are multiples of p equal to false, a task that we pass to a CrossOffMultiples() subroutine. Note below that we need to cast p and n to type float64 as we did in TrivialPrimeFinder().
//SieveOfEratosthenes takes an integer n and returns a slice of n+1
//booleans primeBooleans where primeBooleans[p] is true if p is prime
//and false otherwise.
//It implements the sieve of Eratosthenes approach for finding primes.
func SieveOfEratosthenes(n int) []bool {
primeBooleans := make([]bool, n+1)
// set everything to prime other than primeBooleans[0] and primeBooleans[1]
for k := 2; k <= n; k++ {
primeBooleans[k] = true
}
// now, range over primeBooleans, and cross off multiples of first prime we see, iterating this process.
for p := 2; float64(p) <= math.Sqrt(float64(n)); p++ {
if primeBooleans[p] == true {
primeBooleans = CrossOffMultiples(primeBooleans, p)
}
}
return primeBooleans
}
SieveOfEratosthenes() is now complete, and we can turn to implementing CrossOffMultiples(). This function takes a slice primeBooleans of boolean variables as input, along with an integer p. It returns the updated slice after setting primeBooleans[k] equal to false for every index k that is larger than p and a multiple of p.
//CrossOffMultiples takes a boolean slice and an integer p. It crosses off
//multiples of p, meaning turning these multiples to false in the slice.
//It returns the slice obtained as a result.
func CrossOffMultiples(primeBooleans []bool, p int) []bool {
// let's fill in
}
These indices k are easy to find. We can initialize k equal to 2*p, and then add p to k each time as the postcondition of a for loop whose condition is k <= n. We can write our function as follows.
//CrossOffMultiples takes a boolean slice and an integer p. It crosses off
//multiples of p, meaning turning these multiples to false in the slice.
//It returns the slice obtained as a result.
func CrossOffMultiples(primeBooleans []bool, p int) []bool {
for k := 2*p; k <= n; k += p {
primeBooleans[k] = false // k is composite
}
return primeBooleans
}
STOP: This function has a problem; can you find it?
If we compile main.go, then we will unfortunately obtain a compiler error telling us that n is undefined. When we declare primeBooleans within SieveOfEratosthenes(), we use an input parameter n and construct primeBooleans to have length n+1. However, this parameter’s scope is confined to SieveOfEratosthenes(), and CrossOffMultiples() cannot see it. Fortunately, because we know that the length of primeBooleans is 1 larger than n, we can infer that n is equal to the length of primeBooleans minus 1. This brings us to a final implementation of CrossOffMultiples().
//CrossOffMultiples takes a boolean slice and an integer p. It crosses off
//multiples of p, meaning turning these multiples to false in the slice.
//It returns the slice obtained as a result.
func CrossOffMultiples(primeBooleans []bool, p int) []bool {
n := len(primeBooleans) - 1
for k := 2*p; k <= n; k += p {
primeBooleans[k] = false // k is composite
}
return primeBooleans
}
STOP: Make sure thatSieveOfEratosthenes()is working by calling it on an input of 10 and printing out the resulting slice and ensuring that you get the same result that we did when callingTrivialPrimeFinder()(see ourfunc main()below).
func main() {
fmt.Println("Primes and arrays.")
primeBooleans := SieveOfEratosthenes(10)
fmt.Println(primeBooleans)
}
Listing out primes exemplifies appending to slices in Go
Although we have implemented algorithms to find all prime numbers, there is nevertheless something unsatisfying about what we have done because we are assigning boolean variables to all integers, but we are not producing a list of primes. This task can be completed easily once we have computed primeBooleans — we just need to add all integers p to this list such that primeBooleans[p] is true.
In fact, we mentioned this task in the main text when introducing prime finding algorithms. At that time, we discussed a pseudocode function ListPrimes() that would call SieveOfEratosthenes() as a subroutine and then produce this list by using a function append() that takes an array of integers primeList and an integer p and adds p to the end of primeList.
ListPrimes(n)
primeList ← array of integers of length 0
primeBooleans ← SieveOfEratosthenes(n)
for every integer p from 0 to n+1
if primeBooleans[p] = true
primeList ← append(primeList, p)
return primeList
Go has exactly such a function append(), which takes a slice as well as a variable (of the type corresponding to the slice) and adds this variable to the end of the slice, returning the resulting slice. We use this function to implement ListPrimes() as follows, in which we declare our array of primes primeList to have length 0 and then append to it every time we encounter a prime.
func ListPrimes(n int) []int {
primeList := make([]int, 0)
primeBooleans := SieveOfEratosthenes(n) // remember: primeBooleans will have length n+1
//range over primeBooleans, and append p to primeList if p is prime
for p := 0; p < n+1; p++ {
if primeBooleans[p] == true {
primeList = append(primeList, p)
}
}
return primeList
}
Note:ListPrimes()illustrates a general theme of programming with slices, which is that if we don’t know in advance how long a slice needs to be, we can initiate the slice to have length 0 and append to it each time we need to add an element to the list.
We will also apply the shorthand that we learned in the previous lesson to range over element of primeBooleans in ListPrimes().
func ListPrimes(n int) []int {
primeList := make([]int, 0)
primeBooleans := SieveOfEratosthenes(n) // remember: primeBooleans will have length n+1
//range over primeBooleans, and append p to primeList if p is prime
for p := range primeBooleans {
if primeBooleans[p] == true {
primeList = append(primeList, p)
}
}
return primeList
}
We can now call ListPrimes() within func main() to ensure that it works. The following code should print 2 3 5 7 11 to the console when we compile and run main.go.
func main() {
fmt.Println("Primes and arrays.")
primeList := ListPrimes(11)
fmt.Println(primeList)
}
Timing the two prime finding algorithms
Now that we have implemented two prime finding algorithms, we should time them as we did when comparing our GCD algorithms in the preceding lesson. We can time the two functions for a given n (which we set equal to 1,000,000) by updating func main() as well as the import statements for main.go as follows.
package main
import (
"log"
"time"
"math"
)
func main() {
n := 1000000
start := time.Now()
TrivialPrimeFinder(n)
elapsed := time.Since(start)
log.Printf("TrivialPrimeFinder took %s", elapsed)
start2 := time.Now()
SieveOfEratosthenes(n)
elapsed2 := time.Since(start2)
log.Printf("SieveOfEratosthenes took %s", elapsed2)
}
STOP: Compile and run this code, either on your computer or by using the window below. Try changingnto have smaller and larger values. What do you find?
Once again, we see an astonishing speedup over a trivial algorithm provided by a simple mathematical insight. In this case, why that insight even provides an insight is quite subtle. Rather than checking that each integer is prime, we save a great deal of time by crossing off the multiples of known primes. In one subroutine call, for example, we cross off half the integers up to n corresponding to every multiple of 2, without needing to call IsPrime() on all these integers.
It’s time to practice!
This brings our code alongs for this chapter to a close. Below, we give you the chance to check your work. Once you are finished with this code along, we suggest that you work on this chapter’s fun practice problems that allow you to practice what you have learned throughout this chapter in the context of some unanswered mathematical questions. Or, you can start reading our next chapter on strings and finding hidden messages in DNA.
Check your work from the code along
We provide autograders in the window below (or via a direct link) allowing you to check your work for the following functions:
IsPrime()TrivialPrimeFinder()CrossOffMultiples()SieveOfEratosthenes()ListPrimes()



