Prime Finding Algorithms in Python

Learning objectives

We are now ready to return to our second main narrative in this chapter, finding prime numbers. In the preceding lesson, we saw that Euclid’s algorithm offers a substantial and surprising improvement over a trivial approach. How will the sieve of Eratosthenes fare against a simpler prime finding approach?

Below, we reproduce our pseudocode for TrivialPrimeFinder() and SieveOfEratosthenes() (along with necessary subroutines) from the main text. In this lesson, we will implement these two algorithms and time them.

TrivialPrimeFinder(n)
    primeBooleans ← array of n+1 false boolean variables
    for every integer p from 2 to n
        if IsPrime(p) is true
            primeBooleans[p] ← true
    return primeBooleans

IsPrime(p)
    if p < 2
        return false
    for every integer k between 2 and √p
        if k is a divisor of p
            return false
    return true

SieveOfEratosthenes(n)
    primeBooleans ← array of n+1 true boolean variables
    primeBooleans[0] ← false
    primeBooleans[1] ← false
    for every integer p between 2 and √n
        if primeBooleans[p] = true
            primeBooleans ← CrossOffMultiples(primeBooleans, p)
    return primeBooleans

CrossOffMultiples(primeBooleans, p)
    n ← length(primeBooleans) - 1
    for every multiple k of p (from 2p to n)
        primeBooleans[k] ← false
    return primeBooleans

Code along summary

Setup

Create a new folder called primes in your python/src directory, and then create a new file within the python/src/primes folder called main.py, which we will edit in this lesson.

In main.py, add the following starter code.

def main():
    print("Prime finding.")

if __name__ == "__main__":
    main()

The trivial prime finding algorithm

We are now ready to return to TrivialPrimeFinder() and use what we have learned about lists in the previous code along. Because we pass much of the work to a subroutine is_prime(), this function is quite short. Note that we raise a ValueError if n is less than zero.

def trivial_prime_finder(n: int) -> list[bool]:
    """
    Returns a list of boolean variables storing the primality of each nonnegative integer up to and including n.

    Parameters:
    - n (int): an integer

    Returns:
    list[bool]: a list of boolean variables storing the primality of each nonnegative integer up to and including n.
    """

    if n < 0:
        raise ValueError("n must be nonnegative.")

    prime_booleans = [False] * (n + 1)

    for p in range(2, n + 1):
        prime_booleans[p] = is_prime(p)

    return prime_booleans

We will need to implement is_prime() as well. To do so, we need to have a way to represent the pseudocode line

for every integer k between 2 and √p

To do so, we will use the math module in Python, which has a built in function sqrt(). Note that the second value given to range() is math.sqrt(p) + 1 instead of math.sqrt(p) because ranging in Python goes up to but not including the second element provided to range().

for k in range(2, math.sqrt(p) + 1):

We also know from our work with greatest common divisors in a previous code along that we can check whether k is a divisor of p by checking whether p%k is equal to zero. Our is_prime() function is shown below.

import math # should appear at top of file

def is_prime(p: int) -> bool:
    """
    Test if p is prime.

    Parameters:
    - p (int): an integer

    Returns:
    bool: True if p is prime and False otherwise.
    """

    if p < 2:
        return False

    for k in range(2, math.sqrt(p) + 1):
        if p % k == 0:
            return False
    return True

Unfortunately, this version of is_prime() produces an error because range() takes an int as input. To fix this issue, we will cast the expression math.sqrt(p) + 1 to be an integer. In general, the expression int(x), given a float x as input, returns the integer part of x; for example, int(2.817) is equal to 2, and int(-3.4) is equal to -3.

import math # should appear at top of file

def is_prime(p: int) -> bool:
    """
    Test if p is prime.

    Parameters:
    - p (int): an integer

    Returns:
    bool: True if p is prime and False otherwise.
    """

    if p < 2:
        return False

    for k in range(2, int(math.sqrt(p)) + 1):
        if p % k == 0:
            return False
    return True

Now that we have implemented is_prime(), let’s now call trivial_prime_finder() from def main() and ensure that everything is working properly.

def main():
    print("Primes.")

    prime_booleans = trivial_prime_finder(10)
    print(prime_booleans)

i	prime_booleans[i]
0	False
1	False
2	True
3	True
4	False
5	True
6	False
7	True
8	False
9	False
10	False

Implementing the sieve of Eratosthenes

We are now ready to implement the sieve of Eratosthenes. Below, we reproduce the pseudocode for SieveOfEratosthenes() as well as its subroutine CrossOffMultiples().

SieveOfEratosthenes(n)
    primeBooleans ← array of n+1 true boolean variables
    primeBooleans[0] ← false
    primeBooleans[1] ← false
    for every integer p between 2 and √n
        if primeBooleans[p] = true
            primeBooleans ← CrossOffMultiples(primeBooleans, p)
    return primeBooleans

CrossOffMultiples(primeBooleans, p)
    n ← length(primeBooleans) - 1
    for every multiple k of p (from 2p to n)
        primeBooleans[k] ← false
    return primeBooleans

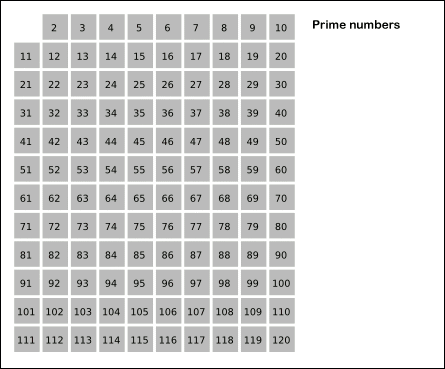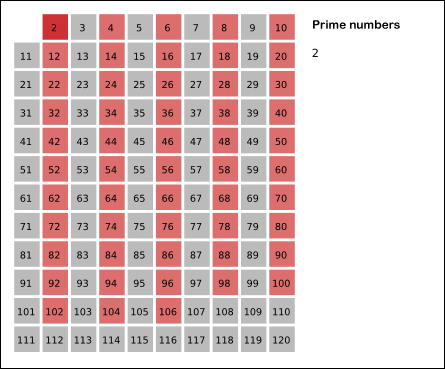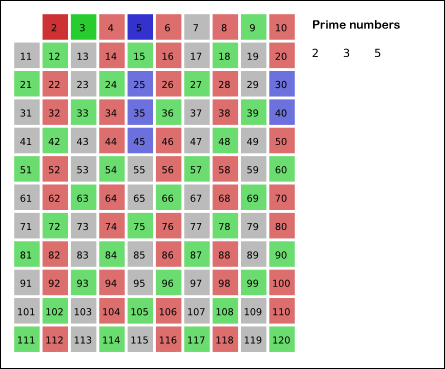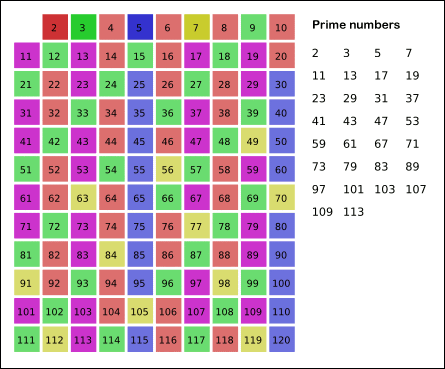
Let us recall how the sieve of Eratosthenes works, as illustrated in the figure below. It first assumes that every integer is prime. Then, over a sequence of steps, it identifies the smallest number in the table that is not composite, and then it “crosses off” all of that number’s factors larger than itself (i.e., sets them to be composite), which is the work of CrossOffMultiples().

Like trivial_prime_finder(), we will need to declare prime_booleans as a list of boolean variables. We know that this list will have length n+1, and so we can declare it to have n+1 True values using the notation prime_booleans = [True] * (n + 1) that we introduced in the previous code along. Let’s start writing our function below.

def sieve_of_eratosthenes(n: int) -> list[bool]:
    """
    Returns a list of boolean variables storing the primality of each nonnegative integer up to and including n,
    implementing the "sieve of Eratosthenes" algorithm.

    Parameters:
    - n (int): an integer

    Returns:
    list: a list of boolean variables storing the primality of each nonnegative integer up to and including n.
    """

    if n < 0:
        raise ValueError("n must be nonnegative.")

    prime_booleans = [True] * (n + 1)
    
    # the meat of our function will go here

    return prime_booleans

We can now initialize prime_booleans[0] and prime_booleans[1] to False.

def sieve_of_eratosthenes(n: int) -> list[bool]:
    """
    Returns a list of boolean variables storing the primality of each nonnegative integer up to and including n,
    implementing the "sieve of Eratosthenes" algorithm.

    Parameters:
    - n (int): an integer

    Returns:
    list[bool]: a list of boolean variables storing the primality of each nonnegative integer up to and including n.
    """

    if n < 0:
        raise ValueError("n must be nonnegative.")

    prime_booleans = [True] * (n + 1)
    prime_booleans[0] = False
    prime_booleans[1] = False
    
    # the meat of our function will go here

    return prime_booleans

We are now ready to implement the engine of the sieve. We use a for loop to range over all p between 2 and √n; note below that we need to cast p ** 0.5 + 1 to have type int as we did in trivial_prime_finder().

def sieve_of_eratosthenes(n: int) -> list[bool]:
    """
    Returns a list of boolean variables storing the primality of each nonnegative integer up to and including n,
    implementing the "sieve of Eratosthenes" algorithm.

    Parameters:
    - n (int): an integer

    Returns:
    list[bool]: a list of boolean variables storing the primality of each nonnegative integer up to and including n.
    """

    if n < 0:
        raise ValueError("n must be nonnegative.")

    prime_booleans = [True] * (n + 1)
    prime_booleans[0] = False
    prime_booleans[1] = False
    
    # now, range over primeBooleans, and cross off multiples of first prime we see, iterating this process.
    for p in range(2, int(math.sqrt(n)) + 1):
        # in progress

    return prime_booleans

Each time through the loop, we ask “Is p prime?” If this is the case (i.e., if prime_booleans[p] is True), then we keep prime_booleans[p] equal to True. We then update our prime_booleans list by looking for all other indices of prime_booleans that are multiples of p, and setting their corresponding values equal to False. We pass off this task to a subroutine cross_off_multiples().

def sieve_of_eratosthenes(n: int) -> list[bool]:
    """
    Returns a list of boolean variables storing the primality of each nonnegative integer up to and including n,
    implementing the "sieve of Eratosthenes" algorithm.

    Parameters:
    - n (int): an integer

    Returns:
    list[bool]: a list of boolean variables storing the primality of each nonnegative integer up to and including n.
    """

    if n < 0:
        raise ValueError("n must be nonnegative.")

    prime_booleans = [True] * (n + 1)
    prime_booleans[0] = False
    prime_booleans[1] = False
    
    # now, range over primeBooleans, and cross off multiples of first prime we see, iterating this process.
    for p in range(2, int(math.sqrt(n)) + 1):
        # is p prime? If so, cross off its multiples
        if prime_booleans[p]:
            prime_booleans = cross_off_multiples(prime_booleans, p)

    return prime_booleans

Our function sieve_of_eratosthenes() is now complete, and we can turn to implementing cross_off_multiples(). This function takes a list prime_booleans of boolean variables as input, along with an integer p. It returns the updated list after setting prime_booleans[k] equal to False for every index k that is both larger than p and a multiple of p. We provide the function signature and docstring below.

def cross_off_multiples(prime_booleans: list[bool], p:int) -> list[bool]:
    """
    Returns an updated list in which all variables in the list whose indices are multiples of p (greater than p) have
    been set to false.

    Parameters:
    - prime_booleans (list): a list of boolean variables storing the primality of each nonnegative integer
    - p (int): an integer

    Returns:
    list[bool]: a list of boolean variables storing the primality of each nonnegative integer up to and including n with
    multiples of p (greater than p) set to false.
    """

    # Let's fill in

We next want to find all indices k that are both larger than p and a multiple of p, which we can do by ranging from 2*p to (not including) n+1, using a step size of p. This can be achieved using for k in range(2 * p, n + 1, p):, as we learned about when discussing for loops.

def cross_off_multiples(prime_booleans: list[bool], p:int) -> list[bool]:
    """
    Returns an updated list in which all variables in the list whose indices are multiples of p (greater than p) have
    been set to false.

    Parameters:
    - prime_booleans (list): a list of boolean variables storing the primality of each nonnegative integer
    - p (int): an integer

    Returns:
    list[bool]: a list of boolean variables storing the primality of each nonnegative integer up to and including n with
    multiples of p (greater than p) set to false.
    """

    for k in range(2 * p, n + 1, p):
        prime_booleans[k] = False
    return prime_booleans    

def main():
    print("Primes.")

    prime_booleans = sieve_of_eratosthenes(10)
    print(prime_booleans)

Unfortunately, when we call sieve_of_eratosthenes(), we obtain a NameError telling us that n is undefined in the line

for k in range(2 * p, n + 1, p):

When we declare prime_booleans within sieve_of_eratosthenes(), we use an input parameter n and construct prime_booleans to have length n+1. However, this parameter’s scope is confined to sieve_of_eratosthenes(), and cross_off_multiples() cannot see it. Fortunately, because we know that the length of prime_booleans is 1 larger than n, we can infer that n is equal to the length of prime_booleans minus 1. This brings us to a final implementation of cross_off_multiples() in which we first set n = len(prime_booleans) - 1.

def cross_off_multiples(prime_booleans: list[bool], p:int) -> list[bool]:
    """
    Returns an updated list in which all variables in the list whose indices are multiples of p (greater than p) have
    been set to false.

    Parameters:
    - prime_booleans (list): a list of boolean variables storing the primality of each nonnegative integer
    - p (int): an integer

    Returns:
    list[bool]: a list of boolean variables storing the primality of each nonnegative integer up to and including n with
    multiples of p (greater than p) set to false.
    """

    n = len(prime_booleans) - 1
    for k in range(2 * p, n + 1, p):
        prime_booleans[k] = False  # k is composite
    return prime_booleans
    

Listing primes exemplifies appending to lists in Python

Although we have implemented algorithms to find all prime numbers, there is nevertheless something unsatisfying about what we have done because we are assigning boolean variables to all integers, but we are not producing a list of primes. This task can be completed easily once we have computed prime_booleans — we just need to create a list containing all integers p such that prime_booleans[p] is True.

In fact, we mentioned this task in the core text when introducing prime finding algorithms. At that time, we discussed a pseudocode function ListPrimes() that would call SieveOfEratosthenes() as a subroutine and then produce this list by using a function append() that takes an array of integers primeList and an integer p and adds p to the end of primeList.

ListPrimes(n)
    primeList ← array of integers of length 0
    primeBooleans ← SieveOfEratosthenes(n)
    for every integer p from 0 to n
        if primeBooleans[p] = true
            primeList ← append(primeList, p)
    return primeList

Python has exactly such a function append(), which applies to lists because (unlike tuples) lists are mutable. Given a list a and an item val that we wish to append to a, we can do so by calling

a.append(val)

We will use this idea to implement ListPrimes() as the following Python function list_primes(), which relies on sieve_of_eratosthenes() as a subroutine. This function illustrates a general theme of programming with lists that we introduced briefly in the previous code along, which is that if we don’t know in advance how long a list needs to be, we can initiate the list to have length 0 and append to it each time we need to add an element to the list.

def list_primes(n: int) -> list[int]:
    """
    List all prime numbers up to and (possibly) including n.

    Parameters:
    - n (int): an integer

    Returns:
    list[int]: a list containing all prime numbers up to and (possibly) including n.
    """

    # first, create an empty list
    prime_list = []

    prime_booleans = sieve_of_eratosthenes(n)
    for p in range(len(prime_booleans)):
        if prime_booleans[p]:
            prime_list.append(p)

    return prime_list

We can now call list_primes() within def main() to ensure that it works. The following code should print [2, 3, 5, 7, 11] to the console when we run main.py.

def main():
    print("Primes.")

    prime_list = list_primes(11)
    print(prime_list)

Timing the two prime finding algorithms

Now that we have implemented two prime finding algorithms, we should time them as we did when comparing our GCD algorithms in a previous code along. We can time the two functions for a given value of n (which we set equal to 1,000,000) by updating def main() as well as the import statements for main.py as follows. Note that, to run the following code, we need to import the time module.

import time

def main():
    n = 1000000

    # timing trivial_prime_finder
    start = time.time()
    trivial_prime_finder(n)
    elapsed_trivial = time.time() - start
    print(f"trivial_prime_finder took {elapsed_trivial:.6f} seconds")

    # timing sieve_of_eratosthenes
    start = time.time()
    sieve_of_eratosthenes(n)
    elapsed_sieve = time.time() - start
    print(f"sieve_of_eratosthenes took {elapsed_sieve:.6f} seconds")

    # compute and print speedup
    if elapsed_sieve > 0:
        speedup = elapsed_trivial / elapsed_sieve
        print(f"Speedup: {speedup:.2f}x faster")

Once again, as the table below demonstrates, we see an astonishing speedup over a trivial algorithm provided by a simple mathematical insight. In this case, why that insight even provides an insight is quite subtle. Rather than checking that each integer is prime, we save a great deal of time by crossing off the multiples of known primes. In one subroutine call, for example, we cross off half the integers up to n corresponding to every multiple of 2, without needing to call is_prime() on all these integers.

n	trivial_prime_finder() Runtime	sieve_of_eratosthenes() Runtime	Speedup
10,000	0.0133 s	0.000871 s	15
100,000	0.226 s	0.00990 s	23
1,000,000	5.01 s	0.104 s	48
10,000,000		0.930 s	60

It’s time to practice!

This brings our code alongs for this chapter to a close. Below, we give you the chance to check your work. Once you are finished with this code along, we suggest that you work on this chapter’s fun practice problems that allow you to practice what you have learned throughout this chapter in the context of some unanswered mathematical questions. Or, you can start reading our next chapter on strings and finding hidden messages in DNA.

Check your work from the code along

We provide autograders in the window below (or via a direct link) allowing you to check your work for the following functions:

• is_prime()
• trivial_prime_finder()
• cross_off_multiples()
• sieve_of_eratosthenes()
• list_primes()

powered by Advanced iFrame

---