Code Along - Simulating an Election from Polling Data in Python

Learning objectives

In this code along, we will use Monte Carlo simulation to estimate the winner of the 2016 US Presidential election using polling data at three different points in time. To do so, we will revisit the SimulateMultipleElections() function that we introduced in the core text, which we reproduce below. This function largely consists of appealing to a SimulateOneElection() subroutine, which returns the electoral college votes for each of two US presidential candidates in a simulated election.

SimulateMultipleElections(pollingData, numTrials, marginOfError)
    winCount1 ← 0
    winCount2 ← 0
    tieCount ← 0
    for numTrials total trials
        votes1,votes2 ← SimulateOneElection(pollingData, marginOfError)
        if votes1 > votes2
            winCount1 ← winCount1 + 1
        else if votes2 > votes1
            winCount2 ← winCount2 + 1
        else (tie!)
            tieCount ← tieCount + 1
    probability1 ← winCount1/numTrials
    probability2 ← winCount2/numTrials
    probabilityTie ← tieCount/numTrials
    return probability1, probability2, probabilityTie

The SimulateOneElection() function examines the polling percentage (for candidate 1) in each state and adds noise to this percentage to reflect the fact that polls can only sample a small portion of the electorate and may be influenced by the effects of random noise.

SimulateOneElection(polls, electoralVotes, marginOfError)
    votes1 ← 0
    votes2 ← 0
    for every key state in polls
        poll ← candidate 1's polling percentage
        adjustedPoll ← AddNoise(poll, marginOfError)
        if adjustedPoll ≥ 0.5 (candidate 1 wins state)
            votes1 ← votes1 + electoralVotes[state]
        else (candidate 2 wins state)
            votes2 ← votes2 + electoralVotes[state]
    return votes1, votes2

As we saw in the code along on simulating craps, the work of generating pseudorandom numbers is passed to a low-level subroutine. In this case, that subroutine is AddNoise(), which takes a polling average and a margin of error and simulates a true polling number with a 95% chance of being within the margin of error. This function requires RandNormal(), a built-in function that generates a pseudorandom decimal according to the standard normal distribution (which has a mean equal to 0 and a standard deviation equal to 1).

AddNoise(poll, marginOfError)
    x ← RandNormal()
    x ← x/2 (95% chance of x being between -1 and 1)
    x ← x * marginOfError (now x is in range)
    return x + poll

Code along summary

Setup

To complete this code along, you will need to build upon the starter code that we provided in the previous code along on parsing election data. Ensure that you have an election directory under your python/src source code folder and that it contains a main.py file, an elections_io.py file (with completed functions from the previous code along), and a data folder containing four data files that are explained further in the previous code along.

Your main.py file should contain the following code from our work on parsing election data, with one additional import statement. We are going to use two functions from elections_io.py: read_electoral_votes() and read_polling_data(). Even though these functions are contained within the same directory as main.py, we need to import them. Because we know which two functions we want to use, we will import them specifically:

from elections_io import read_electoral_votes, read_polling_data

Therefore, main.py should appear as follows. Note that because we have imported it, we can use read_electoral_votes() and read_polling_data() as needed.

from elections_io import read_electoral_votes, read_polling_data

def main():
    print("Let's simulate an election!")

    electoral_vote_file = "data/electoralVotes.csv"
    poll_file = "data/debates.csv"

    # read files and store as dictionaries
    electoral_votes = read_electoral_votes(electoral_vote_file)
    polls = read_polling_data(poll_file)

Writing a function to simulate multiple elections

We start with implementing simulate_multiple_elections(), and we will implement subroutines as we encounter them. Our simulate_multiple_elections() function takes four input parameters:

a dictionary polls that maps the name of each state to that state’s polling percentages of candidate 1 (Clinton), where the polling percentage for candidate 2 (Trump) can be obtained by subtracting candidate 1’s polling percentage from 1;
a dictionary electoral_votes that maps the name of each state to the number of Electoral College votes (as an integer) that the winner of that state receives;
an integer num_trials representing the number of Monte Carlo simulations to run;
a decimal margin_of_error representing the margin of error of all polls, which we assume is a constant.

As for outputs, simulate_multiple_elections() returns three float values, packaged into a Tuple, corresponding to the respective estimated probabilities of candidate 1 winning, candidate 2 winning, and a tie.

def simulate_multiple_elections(
    polls: Dict[str, float],
    electoral_votes: Dict[str, int],
    num_trials: int,
    margin_of_error: float,
) -> Tuple[float, float, float]:
    """
    Simulates multiple elections and calculates winning probabilities.

    Parameters:
    - polls (dict[str, float]): A dictionary of state names to polling percentages for candidate 1.
    - electoral_votes (dict[str, int]): A dictionary of state names to electoral votes.
    - num_trials (int): The number of trials to run.
    - margin_of_error (float): The margin of error in the polls.

    Returns:
    - tuple[float, float, float]: The estimated probabilities of candidate 1 winning,
      candidate 2 winning, and a tie.
    """

    if num_trials <= 0:
        raise ValueError("num_trials must be positive.")
    if margin_of_error < 0:
        raise ValueError("margin_of_error must be non-negative.")

    # to fill in

We will start by declaring three variables win_count1, win_count2, and tie_count, which respectively correspond to the number of simulations won by candidate 1, the number of simulations won by candidate 2, and the number of simulations in which the two candidates tie.

def simulate_multiple_elections(
    polls: dict[str, float],
    electoral_votes: dict[str, int],
    num_trials: int,
    margin_of_error: float
) -> tuple[float, float, float]:
    """
    Simulates multiple elections and calculates winning probabilities.

    Parameters:
    - polls (dict[str, float]): A dictionary of state names to polling percentages for candidate 1.
    - electoral_votes (dict[str, int]): A dictionary of state names to electoral votes.
    - num_trials (int): The number of trials to run.
    - margin_of_error (float): The margin of error in the polls.

    Returns:
    - tuple[float, float, float]: The estimated probabilities of candidate 1 winning,
      candidate 2 winning, and a tie.
    """

    if num_trials <= 0:
        raise ValueError("num_trials must be positive.")
    if margin_of_error < 0:
        raise ValueError("margin_of_error must be non-negative.")

    win_count1 = 0
    win_count2 = 0
    tie_count = 0

    # to fill in

Eventually, we will normalize each of these counts by dividing them by the total number of trials, and then return the resulting ratios.

def simulate_multiple_elections(
    polls: dict[str, float],
    electoral_votes: dict[str, int],
    num_trials: int,
    margin_of_error: float
) -> tuple[float, float, float]:
    """Simulates multiple elections and calculates winning probabilities.

    Parameters:
    - polls (dict[str, float]): A dictionary of state names to polling percentages for candidate 1.
    - electoral_votes (dict[str, int]): A dictionary of state names to electoral votes.
    - num_trials (int): The number of trials to run.
    - margin_of_error (float): The margin of error in the polls.

    Returns:
    - tuple[float, float, float]: The estimated probabilities of candidate 1 winning,
      candidate 2 winning, and a tie.
    """
    if num_trials <= 0:
        raise ValueError("num_trials must be positive.")
    if margin_of_error < 0:
        raise ValueError("margin_of_error must be non-negative.")

    win_count1 = 0
    win_count2 = 0
    tie_count = 0

    # to fill in

    # divide number of wins by number of trials
    probability1 = win_count1 / num_trials
    probability2 = win_count2 / num_trials
    probability_tie = tie_count / num_trials

    return probability1, probability2, probability_tie

We fill in the interior of simulate_multiple_elections() by running num_trials total simulations. Each simulation, we call simulate_one_election(), which will take all of the inputs of simulate_multiple_elections() except for num_trials and return the number of electoral votes for each of candidate 1 and 2 in a simulated election. Based on who has more votes in this simulation (or if there is a tie), we then update the appropriate count variable.

def simulate_multiple_elections(
    polls: dict[str, float],
    electoral_votes: dict[str, int],
    num_trials: int,
    margin_of_error: float
) -> tuple[float, float, float]:
    """
    Simulates multiple elections and calculates winning probabilities.

    Parameters:
    - polls (dict[str, float]): A dictionary of state names to polling percentages for candidate 1.
    - electoral_votes (dict[str, int]): A dictionary of state names to electoral votes.
    - num_trials (int): The number of trials to run.
    - margin_of_error (float): The margin of error in the polls.

    Returns:
    - tuple[float, float, float]: The estimated probabilities of candidate 1 winning,
      candidate 2 winning, and a tie.
    """

    win_count1 = 0
    win_count2 = 0
    tie_count = 0

    # simulate a single election n times and update count each time
    for _ in range(num_trials):
        # simulate one election
        votes1, votes2 = simulate_one_election(
            polls, electoral_votes, margin_of_error)

        # who won?
        if votes1 > votes2:
            win_count1 += 1
        elif votes2 > votes1:
            win_count2 += 1
        else:
            # dreaded tie!
            tie_count += 1

    # divide number of wins by number of trials
    probability1 = win_count1 / num_trials
    probability2 = win_count2 / num_trials
    probability_tie = tie_count / num_trials

    return probability1, probability2, probability_tie

Simulating a single election

We now turn to implementing simulate_one_election(). As we mentioned above, this function takes all of the same parameters as simulate_multiple_elections() except for num_trials. It returns two integers corresponding to the number of electoral college votes for candidate 1 and 2, respectively. We begin by declaring two integers to hold these votes, which we will eventually return.

def simulate_one_election(
    polls: dict[str, float],
    electoral_votes: dict[str, int],
    margin_of_error: float
) -> tuple[int, int]:
    """
    Simulates one election and calculates electoral college votes for each candidate.

    Parameters:
    - polls (dict[str, float]): A dictionary of state names to polling percentages for candidate 1.
    - electoral_votes (dict[str, int]): A dictionary of state names to electoral votes.
    - margin_of_error (float): The margin of error in the polls.

    Returns:
    - tuple[int, int]: The number of electoral college votes for each of the two candidates.
    """
    # basic checks
    if margin_of_error < 0:
        raise ValueError("margin_of_error must be non-negative.")

    college_votes1 = 0
    college_votes2 = 0

    # to fill in

    return college_votes1, college_votes2

simulate_one_election() needs to run the simulation over all states, and we can grab the state names and the current polling value by ranging over the keys and values of polls. We can then access the state’s number of electoral votes with electoral_votes[state].

def simulate_one_election(
    polls: dict[str, float],
    electoral_votes: dict[str, int],
    margin_of_error: float
) -> tuple[int, int]:
    """
    Simulates one election and calculates electoral college votes for each candidate.

    Parameters:
    - polls (dict[str, float]): A dictionary of state names to polling percentages for candidate 1.
    - electoral_votes (dict[str, int]): A dictionary of state names to electoral votes.
    - margin_of_error (float): The margin of error in the polls.

    Returns:
    - tuple[int, int]: The number of electoral college votes for each of the two candidates.
    """
    # basic checks
    if margin_of_error < 0:
        raise ValueError("margin_of_error must be non-negative.")
    if not polls:
        raise ValueError("polls dictionary cannot be empty.")
    if not electoral_votes:
        raise ValueError("electoral_votes dictionary cannot be empty.")

    college_votes1 = 0
    college_votes2 = 0

    # range over all the states, and simulate the election in each one
    for state, polling_value in polls.items():
        # first, let's grab the number of EC votes
        num_votes = electoral_votes[state]

        # to fill in

    return college_votes1, college_votes2

Because the polling value is not a precise estimate, we will first adjust the polling value by adding some randomized noise that is a normally distributed random variable with mean equal to zero and standard deviation equal to half of the polls’ margin of error, which we will pass to a subroutine add_noise().

def simulate_one_election(
    polls: dict[str, float],
    electoral_votes: dict[str, int],
    margin_of_error: float
) -> tuple[int, int]:
    """
    Simulates one election and calculates electoral college votes for each candidate.

    Parameters:
    - polls (dict[str, float]): A dictionary of state names to polling percentages for candidate 1.
    - electoral_votes (dict[str, int]): A dictionary of state names to electoral votes.
    - margin_of_error (float): The margin of error in the polls.

    Returns:
    - tuple[int, int]: The number of electoral college votes for each of the two candidates.
    """
    if margin_of_error < 0:
        raise ValueError("margin_of_error must be non-negative.")
    if not polls:
        raise ValueError("polls dictionary cannot be empty.")
    if not electoral_votes:
        raise ValueError("electoral_votes dictionary cannot be empty.")

    college_votes1 = 0
    college_votes2 = 0

    # range over all the states, and simulate the election in each one
    for state, polling_value in polls.items():
        # first, let's grab the number of EC votes
        num_votes = electoral_votes[state]

        # let's adjust the polling value with some noise
        adjusted_poll = add_noise(polling_value, margin_of_error)

        # to fill in

    return college_votes1, college_votes2

Now that we have an adjusted polling value, we must check whether it is greater than or equal to 0.5. If so, then we can conclude that candidate 1 won the state in this simulation, and otherwise, we can conclude that candidate 2 won the state in this simulation.

def simulate_one_election(
    polls: dict[str, float],
    electoral_votes: dict[str, int],
    margin_of_error: float
) -> tuple[int, int]:
    """
    Simulates one election and calculates electoral college votes for each candidate.

    Parameters:
    - polls (dict[str, float]): A dictionary of state names to polling percentages for candidate 1.
    - electoral_votes (dict[str, int]): A dictionary of state names to electoral votes.
    - margin_of_error (float): The margin of error in the polls.

    Returns:
    - tuple[int, int]: The number of electoral college votes for each of the two candidates.
    """
    college_votes1 = 0
    college_votes2 = 0

    # range over all the states, and simulate the election in each one.
    for state, polling_value in polls.items():
        # first, let's grab the number of EC votes
        num_votes = electoral_votes[state]

        # let's adjust the polling value with some noise
        adjusted_poll = add_noise(polling_value, margin_of_error)

        # who won the state? (based on adjusted number)
        if adjusted_poll >= 0.5:
            college_votes1 += num_votes
        else:
            college_votes2 += num_votes

    return college_votes1, college_votes2

Note: We would obtain the same result if we were instead to check if adjusted_poll is greater than 0.5, because since we will be generating a random decimal number, the chances that adjusted_poll is exactly equal to 0.5 are essentially zero.

Adding random noise to a polling value

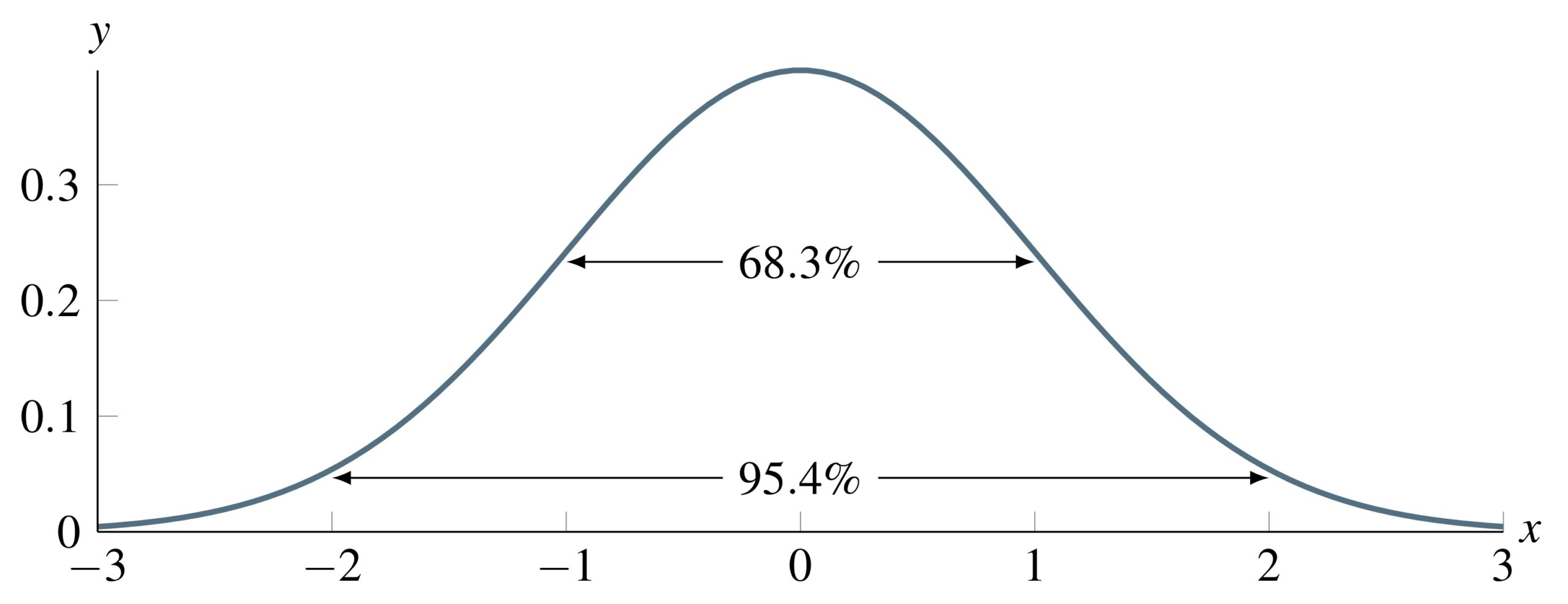
We now turn to implementing add_noise(), which takes as input a polling percentage in a state and the margin of error and returns an adjusted polling percentage corresponding to a simulated polling percentage. We first generate a random number x from the standard normal distribution, reproduced below, which has mean equal to 0 and standard deviation equal to 1. Python implements this with a random.gauss()function in the "random" package.

The standard normal density function. The area under the curve between *x-values of a and b is equal to the probability of generating a pseudorandom number between a and b.*

def add_noise(polling_value: float, margin_of_error: float) -> float:
    """
    Adds random noise to a polling value.

    Parameters:
    - polling_value (float): The polling value for candidate 1.
    - margin_of_error (float): The margin of error.

    Returns:
    - float: An adjusted polling value for candidate 1 after adding random noise.
    """
    if margin_of_error < 0 or polling_value < 0 or polling_value > 1:
        raise ValueError("Invalid polling value or margin of error.")

    x = random.gauss(0, 1)

    # to fill in

Because 95% of draws from a standard normal falls lie between -2 and 2, we can obtain a number having a 95% chance of falling between -1 and 1 by halving x.

import random

def add_noise(polling_value: float, margin_of_error: float) -> float:
    """
    Adds random noise to a polling value.

    Parameters:
    - polling_value (float): The polling value for candidate 1 (between 0 and 1).
    - margin_of_error (float): The margin of error (must be non-negative).

    Returns:
    - float: An adjusted polling value for candidate 1 after adding random noise.
    """
    if margin_of_error < 0 or polling_value < 0 or polling_value > 1:
        raise ValueError("Invalid polling value or margin of error.")

    x = random.gauss(0, 1)
    # x has a ~95% chance of being between -2 and 2

    x /= 2.0
    # x now has a ~95% chance of being between -1 and 1

    # to fill in

We then can ensure that the process of generating x has margin of error equal to margin_of_error by multiplying x by margin_of_error.

import random

def add_noise(polling_value: float, margin_of_error: float) -> float:
    """
    Adds random noise to a polling value.

    Parameters:
        polling_value (float): The polling value for candidate 1 (between 0 and 1).
        margin_of_error (float): The margin of error (non-negative).

    Returns:
        float: An adjusted polling value for candidate 1 after adding random noise.
    """
    if polling_value < 0 or polling_value > 1 or margin_of_error < 0:
        raise ValueError("polling_value must be in [0,1] and margin_of_error must be non-negative.")

    x = random.gauss(0, 1)
    # x has a ~95% chance of being between -2 and 2

    x /= 2.0
    # x has a ~95% chance of being between -1 and 1

    x *= margin_of_error
    # x has a ~95% chance of being between -margin_of_error and +margin_of_error

    # to fill in

We have now obtained our desired noise value, and so we add the value of x to the existing polling value to ensure that the value that we return has mean equal to pollingValue and margin of error equal to marginOfError.

def add_noise(polling_value: float, margin_of_error: float) -> float:
	"""Adds random noise to a polling value.

	Parameters:
		polling_value (float): the polling value for candidate 1, expected between 0.0 and 1.0.
		margin_of_error (float): the margin of error, must be non-negative.

	Returns:
		float: an adjusted polling value for candidate 1 after adding random noise.
	"""
	# parameter checks
	if polling_value < 0.0 or polling_value > 1.0:
		raise ValueError("polling_value must be between 0.0 and 1.0.")
	if margin_of_error < 0.0:
		raise ValueError("margin_of_error must be non-negative.")

	x = random.gauss(0, 1)
	# x has a 95% chance of being between -2 and 2

	x /= 2.0
	# x has a 95% chance of being between -1 and 1

	x *= margin_of_error
	# x has a 95% chance of being between -margin_of_error and +margin_of_error

	return polling_value + x

Running our election simulator

We are now ready to run our Monte Carlo simulation. We revisit our main.py file, which reads in the electoral votes and polling data. The data directory contains three files, and we will begin our work by reading in the first file.

earlyPolls.csv: polls from summer 2016.
conventions.csv: polls from around the Republican and Democratic National Conventions in mid- and late July 2016.
debates.csv: polls from around the presidential debates, in late September through mid-October 2016.

import random  # for generating random numbers

def main():
	"""Runs the election simulation by loading electoral votes and polling data."""
	print("Let's simulate an election!")

	electoral_vote_file = "data/electoralVotes.csv"
	poll_file = "data/debates.csv"

	# read them in and store as dictionaries
	electoral_votes = read_electoral_votes(electoral_vote_file)
	polls = read_polling_data(poll_file)

We next set the number of trials to 1 million and the margin of error to 5%.

def main() -> None:
    """Runs the election simulation with given files, trials, and margin of error."""
    print("Let's simulate an election!")

    electoral_vote_file = "data/electoralVotes.csv"
    poll_file = "data/debates.csv"

    # now, read them in and store as dictionaries
    electoral_votes = read_electoral_votes(electoral_vote_file)
    polls = read_polling_data(poll_file)

    num_trials = 1000000
    margin_of_error = 0.05

    # to fill in

Now that all its inputs are set, we call simulate_multiple_elections() and store the resulting probabilities of each candidate winning (and the probability of a tie). We then print these probabilities to the console.

STOP: After completing main.py with the code below, we are now ready to run our code. In a terminal, navigate to our python/src/election directory. Execute the command python3 main.py (macOS/Linux) or python main.py (Windows). What do you find? Is it what you expected?

def main():
	print("Let's simulate an election!")

	electoral_vote_file = "data/electoralVotes.csv"
	poll_file = "data/debates.csv"

	# now, read them in and store as dictionaries
	electoral_votes = read_electoral_votes(electoral_vote_file)
	polls = read_polling_data(poll_file)

	num_trials = 1000000
	margin_of_error = 0.05

	probability1, probability2, probability_tie = simulate_multiple_elections(
		polls, electoral_votes, num_trials, margin_of_error
	)

	print("Probability of candidate 1 winning:", probability1)
	print("Probability of candidate 2 winning:", probability2)
	print("Probability of tie:", probability_tie)

When we run our code, we obtain a surprising result: Clinton wins 99.9% of the simulations!

Perhaps our simulation is too confident. Let us therefore increase the margin of error to 10%, which produces a very conservative simulation: even if a candidate could be polling at 60% in a state poll, this margin of error implies that there is still a 5% chance of the true polling value being either greater than 70% or less than 50%; that is, there is a 2.5% chance that the other candidate is actually leading.

def main():
	print("Let's simulate an election!")

	electoral_vote_file = "data/electoralVotes.csv"
	poll_file = "data/debates.csv"

	# now, read them in and store as dictionaries
	electoral_votes = read_electoral_votes(electoral_vote_file)
	polls = read_polling_data(poll_file)

	num_trials = 1000000
	margin_of_error = 0.1

	probability1, probability2, probability_tie = simulate_multiple_elections(
		polls, electoral_votes, num_trials, margin_of_error
	)

	print("Probability of candidate 1 winning:", probability1)
	print("Probability of candidate 2 winning:", probability2)
	print("Probability of tie:", probability_tie)

Even with increasing the margin of error, however, Clinton’s dominance over the simulation is still pronounced, as she is leading 98.7% of simulations.

Perhaps Clinton simply had an early lead. To test this hypothesis, let us change the input to read_polling_data() to "conventions.csv", and then compile and run our simulation again.

def main():
	print("Let's simulate an election!")

	electoral_vote_file = "data/electoralVotes.csv"
	poll_file = "data/conventions.csv"

	# now, read them in and store as dictionaries
	electoral_votes = read_electoral_votes(electoral_vote_file)
	polls = read_polling_data(poll_file)

	num_trials = 1000000
	margin_of_error = 0.1

	probability1, probability2, probability_tie = simulate_multiple_elections(
		polls, electoral_votes, num_trials, margin_of_error
	)

	print("Probability of candidate 1 winning:", probability1)
	print("Probability of candidate 2 winning:", probability2)
	print("Probability of tie:", probability_tie)

Clinton’s lead has actually widened — she now wins 99.3% of the simulations!

STOP: Verify that the lead gets even wider when we change the input to read_polling_data() to "debates.csv".

Click Run 👇 to try it!

Note: Here we use 10,000 trials. Try it out with 1 million!

Reflecting on our simulations

These simulations should give us pause. Even though we have what seems like a conservative simulation, we are predicting a Clinton victory very confidently, and our prediction of that victory is more confident than major media outlets, which predicted a Clinton victory in the 60-90 percent range. To understand why our simulation is more confident than more mainstream approaches, we need to pass our work to an epilogue. There, we will reflect on the assumptions of our model and the inherent difficulties that are always present when trying to simulate an election from polls.

We also provide a link below to this chapter’s practice problems, in case you would like to go ahead and start practicing what you have learned in the chapter.

Visit Chapter 2 Practice Problems

Read the Epilogue

Check your work from the code along

We now provide autograders in the window below (or via a direct link) allowing you to check your work for the following functions:

add_noise()
simulate_one_election()
simulate_multiple_elections()

Simulating an Election from Polling Data in Python